Leptonen-Modell
Elektron, Myon, Tauon und Neutrinos
Ein neuartiges String-Modell trägt die Eigenschaften der Leptonen
Durch die Lösung des ›Problems der Zeit‹ lässt sich mit Hilfe der First-Principles die Struktur der Leptonen-Strings verstehen
| ▾ | Notizen |
Zu untersuchende Eigenschaften
• Phasenzahl bzw. Wellenanzahl
– Elektronen-Radius: Passt der Elektronen-Radius, der wohl über das elektromagnetische Feld des Elektrons berechnet werden kann, in dieses Modell? Siehe Wikipedia: Elektron, Klassischer Radius und Punktförmigkeit. Kann die Phasenzahl bzw. Wellenanzahl hiermit in Zusammenhang gebracht werden?
– Feinstrukturkonstante: Kann die Phasenzahl bzw. Wellenanzahl mit der Feinstrukturkonstanten in Zusammenhang gebracht werden? Das sieht so aus. »Sommerfeld definierte sie ursprünglich als das Verhältnis der Bahngeschwindigkeit des Elektrons im Grundzustand des Bohrschen Wasserstoffatoms zur Lichtgeschwindigkeit im Vakuum[2].« Siehe Wikipedia: Feinstrukturkonstante
• Magnetisches Moment des Elektronen-Spins, siehe Wikipedia, Elektron, Eigenschaften.
• Elektrisches Dipolmoment des Elektrons, siehe Wikipedia: Elektron, Klassischer Radius und Punktförmigkeit.
– Hier geht es darum, inwieweit das Massenzentrum dem Zentrum des elektrischen Feldes entspricht.
– Im Leptonen-Modell sollten beide Zentren extrem nahe beieinander liegen, wie es die Experimente bestätigen.
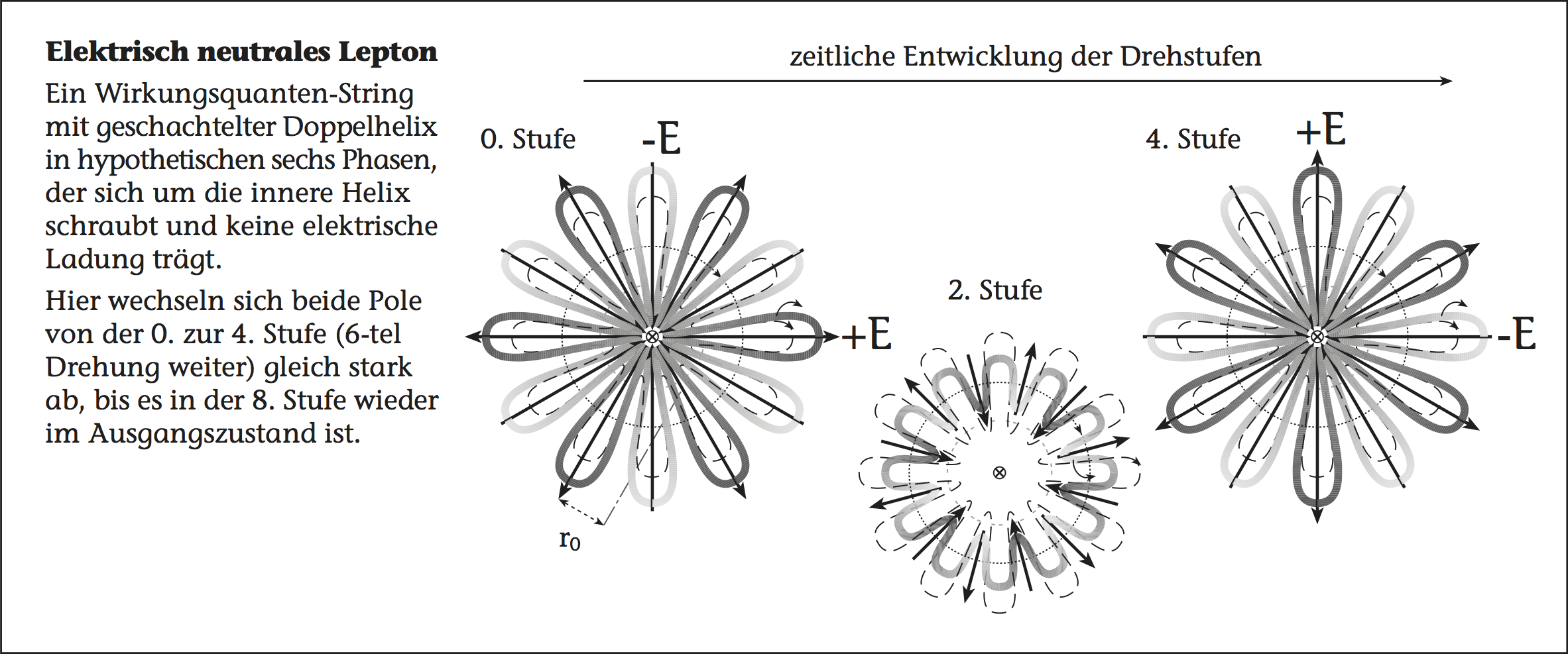
Leptonen kommen in der Natur in geladener und ungeladener Form vor. Geladene Leptonen sind das Elektron/Positron,
das Myon und das Tauon. Die ungeladenen Leptonen sind die entsprechenden .
In der hier beschriebenen Quanten-Fluss-Theorie bestehen alle Leptonen aus einem
Wirkungsquanten-String,
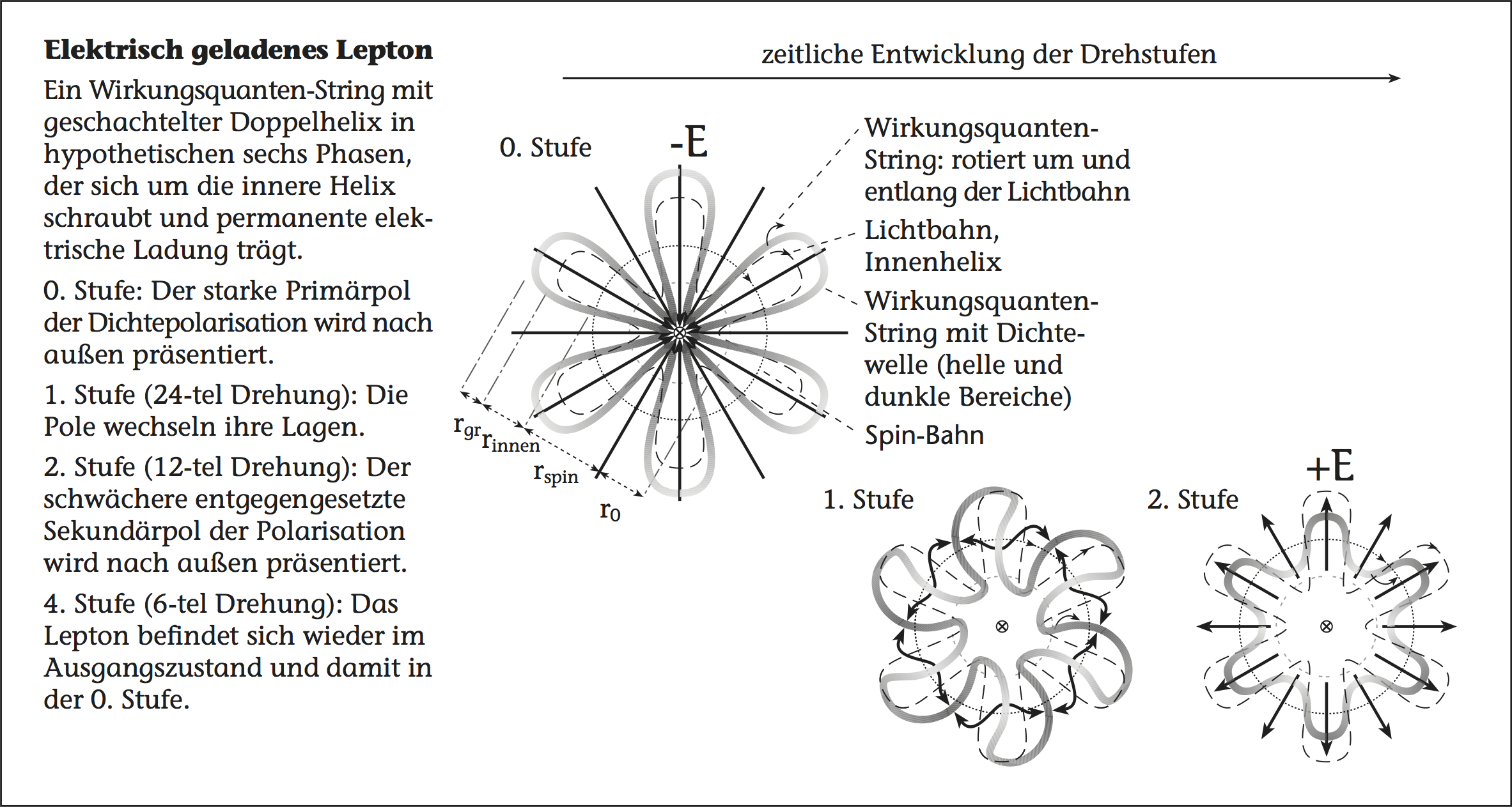
der in asymmetrischer Form mit drei Spins rotiert. Die folgende
und die veranschaulichen ein geladenes Lepton mit hypothetischen acht
wellenförmigen Phasen.
|
Wieviele Phasen das Lepton wirklich besitzt ist noch nicht geklärt. Wie man aus den in der Natur beobachteten Teilchenumwandlungen durch die elektroschwache Wechselwirkung erkennen kann, besitzen alle Leptonen und Quarks die gleiche Phasenzahl. Diese ist mit einem neuen, inneren verknüpft, der offenbar einer globalen Erhaltung unterliegt.
Die String-Struktur und deren Bewegung gibt alle Teilcheneigenschaften, wie sowie und , wider und ist sogar in der Lage die Einsteinschen Formeln der Gravitation durch die Einführung einer herzuleiten.
Wie bei den Photonen besteht der String aus Wirkungsquanten, die mittels ihrer Wechselwirkungskegel – ein sich ausbreitendes Sombrero-Potenzial – miteinander verbunden sind. Die String-Spannung ist durch die (Quantenchromodynamik) oder anders gesagt durch die starke Feldkonstante(Verweise) bestimmt. Auf diese Weise sind alle Grundkräfte der Physik involviert.
Die Gestalt einer helixförmigen Doppelspirale für die String-Bewegung ergibt sich aus der Lösung des ›Problems der Zeit‹ in der Quanten-Fluss-Theorie durch die Differenzierung des heutigen Zeitbegriffs in die Begriffe sowie durch die experimentellen Beobachtungen, die einst in das heutige Standardmodell der Teilchenphysik mündeten.
→
Lösung des ›Problems der Zeit‹ |
|
Vereinheitlichung der Physik durch ein neues Verständnis der Zeit
Das Modell der Quanten-Fluss-Theorie basiert auf einem neuen, auf einem strukturellen Verständnis der Zeit, welches entscheidend dazu beiträgt, die Physik zu vereinheitlichen.
Denn die Frage ist, wie kann es sein, dass ein Elementarteilchen schneller schwingt, wenn seine Gravitationsuhr langsamer läuft, es langsamer altert?
Berücksichtigen wir nicht die Strukturen in einem System, so erscheint es, als sollten auch alle Schwingungen langsamer ablaufen, wenn die ihnen zugrundeliegende Zeit langsamer läuft. Betrachten wir diesen Zusammenhang im Modell der Quanten-Fluss-Theorie, so stellen wir fest, dass hier die Zeit der Allgemeinen Relativitätstheorie nicht die ganz direkte Grundlage genau dieser Schwingungen der Elementarteilchen ist.
Der scheinbare Widerspruch des ›Problems der Zeit‹, wonach höhere Gravitation zu langsamer laufender Zeit und gleichzeitig zu einer höheren De-Broglie-Frequenz – also einer schnelleren Schwingung – der Elementarteilchen führt, wird gelöst, indem ein fraktales, hierarchisches Verständnis der Zeit eingeführt und jede dieser Zeit-Ebenen als Veränderung und damit als bestimmter Aspekt von struktureller Bewegung verstanden wird.
Am Beispiel des Leptonen-Modells (siehe ) veranschaulicht, ist die konstante Geschwindigkeit der rot gefärbten Wirkungsquanten des Leptonen-Strings der alles bestimmende Zeitgeber, der so im einfachsten Fall dargestellten unterliegenden Zeit-Ebene. Die in diesem Modell vereinfachend als feinste Strukturebene angenommene Bewegung der Wirkungsquanten fungiert damit als Normaluhr, die überall im Raum gleich läuft.
Nach Albert Einsteins Allgemeiner Relativitätstheorie ist hingegen das ›Prinzip der Lichtuhr‹ für die zeitlichen Abläufe in einem Elementarteilchen grundlegend. Im Leptonen-Modell ist das ›Prinzip der Lichtuhr‹ durch die Parallelbewegung der Wirkungsquanten zur grünen Lichtbahn realisiert, durch den Gang ihrer Helixspiralbewegung. Dieser Bewegungsanteil entlang der grünen Lichtbahn entspricht der Lichtgeschwindigkeit der Allgemeinen Relativitätstheorie im 3-dimensionalen Raum. Abgrenzend zur Zeit-Ebene der Normaluhr wird diese Zeit-Ebene in der Quanten-Fluss-Theorie als Alterung bezeichnet. Die Alterung ist folglich ein anderer Aspekt der Bewegung und eine andere Form der Zeit, der mit der Gangweite der Wellen der Wirkungsquanten-Bahn um die Lichtbahn variiert.
Umso schneller sich das Lepton im Raum bewegt, desto langsamer ist die Geschwindigkeit der Wirkungsquanten entlang der Lichtbahn.
Entsprechend ist die Alterung des Leptons bei Bewegung langsamer, wie wir es aus der Speziellen Relativitätstheorie kennen.
Ähnliches gilt, wenn sich ein Lepton einem Gestirn mit großer Masse nähert. Seine Alterung läuft langsamer und die Bewegung der Wirkungsquanten entlang der Lichtbahn entspricht seiner Gravitationsuhr. Diese geht umso langsamer, je größer der ist, in dem sich das Lepton befindet. so wie wir es aus der Allgemeinen Relativitätstheorie kennen.
Die De-Broglie-Frequenz eines Leptons, die für seine Energie steht, entspricht nun der Rotationsfrequenz des Wirkungsquanten-Strings um die grüne Lichtbahn. Aufgrund der konstanten Wirkungsquanten-Geschwindigkeit und bei gleich bleibendem Rotationsradius muss eine niedrigere Lichtgeschwindigkeit im 3-dimensionalen Raum zu einem engeren Gang der Helixspiralbahn der Wirkungsquanten und damit, wie bei Licht-Photonen, zu einer höheren Rotationsfrequenz führen.
→
| |
Naturphilosophie der Mechanik |
|
Naturphilosophische Analyse des Leptonen-Modells
←
Um die verschiedenen Leptonen aus Perspektive der Quanten-Fluss-Theorie ähnlich den Photonen beschreiben zu können, ist es notwendig, uns sowohl die dafür entscheidenden Grundlagen, die First-Principles der neuen Physik, als auch ihre beobachteten Eigenschaften vor Augen zu führen.
Leptonen kommen in der Natur in geladener und ungeladener Form vor. sind das Elektron, das Myon und das Tauon sowie das Positron, als Antiteilchen des Elektrons, und die Antiteilchen zum Myon und Tauon. Die ungeladenen Leptonen sind die entsprechenden .
Hier eine Liste ihrer beobachteten Eigenschaften:
| • |
elektrisch positiv oder negativ geladen sowie ungeladen |
| • |
schwache Ladung |
| • |
keine starke Ladung |
| • |
Ruhemasse (Materieinhalt) |
| • |
Spin |
| • |
magnetisches Moment des Spins |
Wenn wir einen Weg finden wollen, diese Eigenschaften prinzipiell in einem neuen Modell des Leptons der hier entwickelten neuen Physik darzustellen, dann ist es entscheidend, zu welchen entsprechenden First-Principles die aufgelisteten Eigenschaften passen sollten. Folgende First-Principles kommen für mich dabei in Betracht:
| • |
Strukturprinzip |
| • |
Eigenschaftsprinzip |
| • |
String-Prinzip |
| • |
Abzählprinzip |
| • |
Bewegungsprinzip |
| • |
Existenzprinzip |
| • |
›Prinzip der Lichtuhr‹ |
| • |
|
| • |
Regelprozess-Prinzip |
Wir können die beobachteten Eigenschaften den Prinzipien folgendermaßen zuordnen:
| • |
Spin (Drehimpuls) |
| • |
Keine starke Ladung |
| • |
Elektrische Ladung |
| • |
Magnetisches Moment des Spins |
| • |
Schwache Ladung |
| • |
Ruhemasse |
All dies wird für den Fall einer positiven elektrischen Ladung in der zusammengebracht.
Erste Analyse der Mechanik und Funktion
Dies gelingt indem ein Wirkungsquanten-String (symbolisiert durch rote Kugeln) mit abschnittsweise unterschiedlicher Dichte um die Linie (grün) einer in sich geschlossenen Helixspirale rotiert. Während seiner Rotation bewegt sich der String mit Lichtgeschwindigkeit parallel zu der grünen Linie, so dass diese Bewegung als Lichtuhr fungiert. Die grüne Linie bezeichne ich aus diesem Grund als Lichtbahn.
Gleichzeitig rotieren die Wirkungsquanten ebenfalls mit Lichtgeschwindigkeit um die Lichtbahn. Insgesamt bewegen sie sich auf einer helixförmigen Spiralbahn um die Lichtbahn, ähnlich wie bei Photonen, die sich ihrerseits um den blauen Kreis der Spin-Bahn windet.
In der werden die dichteren Stellen des Strings beim Entfalten nach außen gerichtet, während die weniger Dichten Stellen zum Zentrum weisen. Dies stellt eine schwingende elektrische Ladung dar, bei der der dominante Pol nach außen präsentiert wird.
Die Umkehrung der nach außen gerichteten Polarisierung gibt es nur bei den neutralen Leptonen. Aber bei den geladenen Leptonen gibt es die Umkehrung nicht in nennenswertem Maße, weil sich ihre Struktur im Moment der Umkehrung zusammenfaltet.
Mechanik des Leptonen-Wirkungsquanten-Strings
Die Berechnung der verschiedenen Spins des Leptonen-Modells führen wir im folgenden Abschnitt durch.
→
| |
Berechnung der String-Mechanik |
|
Die Mechanik des Leptonen-Wirkungsquanten-Strings
←
Die folgenden Formeln werden bei der Berechnung des Leptonen-Modells als grundsätzlich gültig angenommen:
Die allgemeine Wellengleichung ist gegeben durch die Geschwindigkeit c,
die Frequenz f und die Wellenlänge λ mit
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { c\;\;\;=\;\;\;f \cdot \lambda \;\; . } \] | (Lep.Mod.1) |
Die Energie Eele eines Elementarteilchens ist durch seine De-Broglie- Frequenz fele gegeben mit
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { E_{ele}\;\;\;=\;\;\;h \cdot f_{ele} \;\; . } \] | (FP.2) |
Die Energie-Masse-Äquivalenz ist gegeben mit
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { E\;\;\;=\;\;\;m \cdot {_{\raise -.3ex 0}c^{2}} \;\; . } \] | (FP.3) |
Generell gehen wir davon aus, dass die De-Broglie-Frequenz fele eines Elementarteilchens eine Rotation oder Schwingung von einem bestimmten Zustand zum nächsten von diesem ununterscheidbaren ist. Das bedeutet, dass bei einem Schwingungsdurchgang mit der Spin-Rotationsgeschwindigkeit c nicht unbedingt der gesamte String einmal in der Ebene des Haupt-Spins um den Teilchenschwerpunkt rotiert; die Wellenlänge \( \lambda \) also nur einem Teil des Spin-Umfangs entspricht.
In der ist dementsprechend eine Teilchen-Schwingung auch nur eine Teilrotation des Strings in Haupt-Spin-Richtung, also um das Zentrum entlang der blauen Bahn. Dies ermöglicht eine komplexe Struktur der String-Schwingung, durch die der bei Leptonen – oder genereller bei Fermionen – beobachtete Spin von \( ½ \hbar \) erklärbar wird. Auch wird durch die im Modell enthaltene Kombination verschachtelter Helixspiralbewegungen die Schwingung einer verständlich. Dies entspricht der negativen elektrischen Ladung des Elektrons oder seines Antiteilchens Positron, sowie deren schwereren Schwester- und Bruderteilchen: Myon, Tauon und so weiter; und im neutralen Fall den verschiedenen Neutrino-Arten.
Ansatz der Mechanik
Um die Struktur formal zu beschreiben brauchen wir verschiedene Kennzahlen, die einen Leptonen-String auszeichnen:
Wir beginnen mit der Anzahl der elektrischen Feldstärken-Pole npol im String. Diese entsprechen den Wechseln zwischen dichter und weniger dicht mit Wirkungsquanten besetzten Stellen des Strings. Bei geladenen Leptonen-Strings kommt ein Feldstärken-Polwechsel auf eine Lichtbahn-Welle, sodass immer die gleichen Feldstärken-Pole nach außen und die anderen nach innen präsentiert werden (npolwel = 1), wodurch die Teilchen im zeitlichen Mittel elektrisch geladen erscheinen. Bei neutralen Leptonen-Strings verteilt sich ein Feldstärken-Polwechsel auf zwei Lichtbahn-Wellen, sodass gleichzeitig die beiden unterschiedlichen Feldstärken-Pole nach innen (außen?) präsentiert werden (npolwel = 2), was die neutralen Leptonen-Strings bei zunehmender Distanz von deren Schwerpunkt sehr schnell völlig elektrisch neutral erscheinen lässt. Multipliziert mit der Wellenanzahl der grünen Lichtbahn je Feldstärken-Polwechsel npolwel bestimmen sie die gesamte Lichtbahn-Wellenanzahl nwel:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { n_{wel}\;\;\;=\;\;\;n_{pol} \cdot n_{polwel} } \] | (Lep.Mod.2) |
| ▾ | Notizen |
Fragestellungen zur Entwicklung des Modells
Wie stehen nwel, npol und npolwel mit dem Unterschied zwischen den Neutrinos und den geladenen Leptonen im Zusammenhang?
Ladung
• geladen: npolwel = 1
• neutral: npolwel = 2
• neutral: Ladungspole nach innen oder nach außen, Teilchen und Antiteilchen(?), starker Strukturunterschied(!), CP-Verletzung(?), bestimmte Reaktionen gibt es nicht mit links- oder rechtshändigen Neutrinos(?)
Frequenz
• »Generell gehen wir davon aus, dass die De-Broglie-Frequenz fele eines Elementarteilchens eine Rotation oder Schwingung von einem bestimmten Zustand zum nächsten von diesem ununterscheidbaren ist.«
• npolwel = 2 führt dazu, dass ein wirklich ununterscheidbarer Zustand erst nach zwei Durchgängen von fele erreicht wird.
• Beide Zustände sind aber nahezu ununterscheidbar.
• Was bedeutet dies für das Modell?
Wenn sich, wie gesagt, der Wirkungsquanten-String entlang der grünen Lichtbahn mit Lichtgeschwindigkeit 0c bewegt, dann bewegt er sich, projiziert auf den blauen Kreis der Spin-Bahn, im Mittelwert mit der Spin-Geschwindigkeit cspin, wobei cspin < 0c gilt.
Sei fele die Frequenz der String-Schwingungen und λwel die
Lichtbahn-Länge einer Lichtbahn-Welle, dann ergibt sich nach
Formel für
Weiterhin können wir aus dem Radius rspin der blauen Spin-Bahn und der Anzahl der Wellensegmente nwel über den gesamten String die Länge eines Wellensegmentes zu
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \lambda_{wel}\;\;\;=\;\;\;\frac{ 2 \pi \cdot r_{spin} }{ n_{wel} } } \] | (Lep.Mod.5) |
berechnen. So ergibt sich durch Einsetzen die Frequenz
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}f_{ele}\;\;\;=\;\;\;\frac{ c_{spin} }{ \frac{ 2 \pi \cdot r_{spin} }{ n_{wel} } } } \] | (Lep.Mod.6) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f_{ele}\;\;\;=\;\;\;c_{spin} \cdot \frac{ n_{wel} }{ 2 \pi \cdot r_{spin} } } \] | (Lep.Mod.7) | ||
der String-Schwingungen.
Durch Gleichsetzen der Energieformeln
und erhalten wir:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}h \cdot f_{ele}\;\;\;=\;\;\;m_{ele} \cdot {_{\raise -.3ex 0}c^{2}} } \] | (Lep.Mod.8) |
Nun können wir in die vorstehende Formel die davor hergeleitete Formel einsetzen und erhalten:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}h \cdot c_{spin} \cdot \frac{ n_{wel} }{ 2 \pi \cdot r_{spin} }\;\;\;=\;\;\;m_{ele} \cdot {_{\raise -.3ex 0}c^{2}} } \] | (Lep.Mod.9) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}c_{spin}\;\;\;=\;\;\;m_{ele} \cdot {_{\raise -.3ex 0}c^{2}} \cdot \frac{ 2 \pi \cdot r_{spin} }{ h \cdot n_{wel} } } \] | (Lep.Mod.10) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}c_{spin}\;\;\;=\;\;\;\frac{ r_{spin} \cdot m_{ele} \cdot {_{\raise -.3ex 0}c^{2}} }{ \hbar \cdot n_{wel} } } \] | (Lep.Mod.11) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{spin} \cdot m_{ele}\;\;\;=\;\;\;c_{spin} \cdot \frac{ \hbar \cdot n_{wel} }{ {_{\raise -.3ex 0}c^{2}} } } \] | (Lep.Mod.12) | ||
Weil der Spin-Radius rspin entlang des Strings variiert und hier gemittelt ist, ist zu beachten, dass auch die Geschwindigkeit cspin entlang der Spin-Bahn variiert und ebenfalls vereinfachend gemittelt ist. Dass rspin und cspin Mittelungen sind, spielt keine große Rolle, denn die mit ihnen verbundenen gemessenen Größen sind statistischer Natur.
Entscheidend für ein Modell, dass die Physik vereinheitlicht, ist die Realisierung der wesentlichen Eigenschaften der zu vereinheitlichenden Theorien: der Allgemeinen Relativitätstheorie und der Quantenphysik. Mit der Parallelbewegung der Wirkungsquanten zur grünen Lichtbahn realisiert das Modell das ›Prinzip der Lichtuhr‹, das eine wesentliche Eigenschaft der Allgemeinen Relativitätstheorie ist. Mit der Rotation des Wirkungsquanten-Strings um die Lichtbahn realisiert das Modell die De-Broglie-Frequenz des Leptonen-Strings, eine wesentliche Eigenschaft der Quantenphysik.
Die beiden genannten, im Modell realisierten wesentlichen Eigenschaften lösen das oben geschilderte , dass nach meiner Analyse der Vereinheitlichung der Physik im Wege steht. Gemeinsam mit dem beobachteten Leptonen-Spin und seiner Masse berechnen wir jetzt wichtige Eigenschaften des Leptonen-Modells.
Ansatz der konkreten Berechnung der Modelleigenschaften
Ausgangspunkt ist der in Experimenten beobachtete Leptonen-Spin
| ▾ | Notizen |
• Die Beobachtung eines Leptonen-Spins von \( ½ \hbar \) kann durch die Aufspaltung der Photonen-Spins strukturell mechanisch begründet werden.
Wir nutzen nun die experimentelle und in der Quantenphysik zentrale Beobachtung, dass Leptonen den Spin \( ½ \hbar \) tragen:
Im entwickelten Modell wird der Leptonen-Spin slep als realer Drehimpuls verstanden, der sich aus der Masse mlep seines Strings
in Bezug auf dessen mittleren Rotationsradius rspin und seine mittlere Geschwindigkeit cspin zu
berechnet.
Ersetzen wir hierin das Produkt aus Spin-Radius und Masse rspin ⋅ mlep mit Hilfe von Formel , dann erhalten wir:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\frac{ 1 }{ 2 } \hbar\;\;\;=\;\;\;c_{spin} \cdot \frac{ \hbar \cdot n_{wel} }{ {_{\raise -.3ex 0}c^{2}} } \cdot c_{spin} } \] | (Lep.Mod.16) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ 1 }{ 2 } \hbar \cdot \frac{ {_{\raise -.3ex 0}c^{2}} }{ \hbar \cdot n_{wel} }\;\;\;=\;\;\;c_{spin}^{2} } \] | (Lep.Mod.17) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}c_{spin}\;\;\;=\;\;\;\sqrt{ \frac{ {_{\raise -.3ex 0}c^{2}} }{ 2 \cdot n_{wel} } } } \] | (Lep.Mod.18) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}c_{spin}\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}c} }{ \sqrt{ 2 \cdot n_{wel} } } } \] | (Lep.Mod.19) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{\raise -.3ex 0}c}\;\;\;=\;\;\;\sqrt{ 2 \cdot n_{wel} } \cdot c_{spin} } \] | (Lep.Mod.20) | ||
Demnach ist die mittlere Spin-Geschwindigkeit cspin ausschließlich von der Wellenzahl nwel abhängig.
Zur mittleren Rotationsgeschwindigkeit clicht,rot des Strings projiziert auf die grüne Lichtbahn, also entlang der beziehungsweise parallel zur grünen Spirale um die blaue Spin-Bahn, gelangen wir aufgrund der senkrechten Orientierung des Lichtbahn-Radius rlicht,rot zur Spin-Bahn über den Pythagoras:
Die Geschwindigkeit des Strings parallel zur Lichtbahn ist, wie oben geschildert,
per Definition die Lichtgeschwindigkeit 0c:
Wir setzen für cspin Formel und anschließend für die Lichtgeschwindigkeit 0c Formel ein und erhalten
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}c_{licht,rot}\;\;\;=\;\;\;\sqrt{ {_{\raise -.3ex 0}c^{2}} - \left( \frac{ {_{\raise -.3ex 0}c} }{ \sqrt{ 2 \cdot n_{wel} } } \right)^{2} } } \] | (Lep.Mod.23) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}c_{licht,rot}\;\;\;=\;\;\;\sqrt{ {_{\raise -.3ex 0}c^{2}} - \frac{ {_{\raise -.3ex 0}c^{2}} }{ 2 \cdot n_{wel} } } } \] | (Lep.Mod.24) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}c_{licht,rot}\;\;\;=\;\;\;\sqrt{ 1 - \frac{ 1 }{ 2 \cdot n_{wel} } } \cdot {_{\raise -.3ex 0}c} } \] | (Lep.Mod.25) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}c_{licht,rot}\;\;\;=\;\;\;\sqrt{ 1 - \frac{ 1 }{ 2 \cdot n_{wel} } } \cdot \sqrt{ 2 \cdot n_{wel} } \cdot c_{spin} } \] | (Lep.Mod.26) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}c_{licht,rot}\;\;\;=\;\;\;\sqrt{ \left( 1 - \frac{ 1 }{ 2 \cdot n_{wel} } \right) \cdot 2 \cdot n_{wel} } \cdot c_{spin} } \] | (Lep.Mod.27) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}c_{licht,rot}\;\;\;=\;\;\;\sqrt{ 2 \cdot n_{wel} - 1 } \cdot c_{spin} } \] | (Lep.Mod.28) | ||
für die auf die grüne Lichtbahn projizierte Rotationsgeschwindigkeit um die blaue Spin-Bahn.
Mit Hilfe der allgemeinen Wellengleichung können wir jetzt formulieren, wie die auf die grüne Lichtbahn projizierte Rotationsgeschwindigkeit clicht,rot um die blaue Spin-Bahn und ihr Rotationsradius rlicht,rot mit der De-Broglie-Frequenz fele des Leptons in Zusammenhang stehen. Denn wie in der zu erkennen ist, rotiert der Leptonen-String ein Mal um die Lichtbahn, während er auch ein Mal um die Spin-Bahn rotiert. Beide Rotationsfrequenzen sind identisch:
Sei die Wellenlänge durch
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \lambda_{licht,rot}\;\;\;=\;\;\;2 \pi \cdot r_{licht,rot} } \] | (Lep.Mod.29) |
gegeben, so können wir die allgemeine Wellengleichung hierauf anpassen mit:
Durch ersetzen der Rotationsfrequenz fele mittels Formel und von clicht,rot mittels der vorstehenden Formel kommen wir zu
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}c_{licht,rot}\;\;\;=\;\;\;c_{spin} \cdot \frac{ n_{wel} }{ 2 \pi \cdot r_{spin} } \cdot 2 \pi \cdot r_{licht,rot} } \] | (Lep.Mod.32) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}c_{licht,rot}\;\;\;=\;\;\;c_{spin} \cdot \frac{ n_{wel} }{ r_{spin} } \cdot r_{licht,rot} } \] | (Lep.Mod.33) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\sqrt{ 2 \cdot n_{wel} - 1 } \cdot c_{spin}\;\;\;=\;\;\;c_{spin} \cdot \frac{ n_{wel} }{ r_{spin} } \cdot r_{licht,rot} } \] | (Lep.Mod.34) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sqrt{ 2 \cdot n_{wel} - 1 }\;\;\;=\;\;\;\frac{ n_{wel} }{ r_{spin} } \cdot r_{licht,rot} } \] | (Lep.Mod.35) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ \sqrt{ 2 \cdot n_{wel} - 1 } }{ \frac{ n_{wel} }{ r_{spin} } }\;\;\;=\;\;\;r_{licht,rot} } \] | (Lep.Mod.36) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{licht,rot}\;\;\;=\;\;\;\frac{ \sqrt{ 2 \cdot n_{wel} - 1 } }{ n_{wel} } \cdot r_{spin} } \] | (Lep.Mod.37) | ||
für den Rotationsradius der Lichtbahn um die Spin-Bahn.
Aus Formel können wir durch einsetzen von Formel für den mittleren Spin-Radius rspin folgende Formel herleiten:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { r_{spin} \cdot m_{ele}\;\;\;=\;\;\;c_{spin} \cdot \frac{ \hbar \cdot n_{wel} }{ {_{\raise -.3ex 0}c^{2}} } } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{spin}\;\;\;=\;\;\;c_{spin} \cdot \frac{ \hbar \cdot n_{wel} }{ m_{ele} \cdot {_{\raise -.3ex 0}c^{2}} } } \] | (Lep.Mod.38) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}r_{spin}\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}c} }{ \sqrt{ 2 \cdot n_{wel} } } \cdot \frac{ \hbar \cdot n_{wel} }{ m_{ele} \cdot {_{\raise -.3ex 0}c^{2}} } } \] | (Lep.Mod.39) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{spin}\;\;\;=\;\;\;\sqrt{ \frac{ n_{wel}^{2} }{ 2 \cdot n_{wel} } } \cdot \frac{ \hbar }{ m_{ele} \cdot {_{\raise -.3ex 0}c} } } \] | (Lep.Mod.40) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{spin}\;\;\;=\;\;\;\sqrt{ \frac{ n_{wel} }{ 2 } } \cdot \frac{ \hbar }{ m_{ele} \cdot {_{\raise -.3ex 0}c} } } \] | (Lep.Mod.41) | ||
Unser Ergebnis für rspin in die zuvor entwickelte Formel eingesetzt liefert uns für den mittleren Rotationsradius der Lichtspirale
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}r_{licht,rot}\;\;\;=\;\;\;\frac{ \sqrt{ 2 \cdot n_{wel} - 1 } }{ n_{wel} } \cdot \sqrt{ \frac{ n_{wel} }{ 2 } } \cdot \frac{ \hbar }{ m_{ele} \cdot {_{\raise -.3ex 0}c} } } \] | (Lep.Mod.42) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{licht,rot}\;\;\;=\;\;\;\sqrt{ \frac{ 2 \cdot n_{wel} - 1 }{ n_{wel}^{2} } } \cdot \sqrt{ \frac{ n_{wel} }{ 2 } } \cdot \frac{ \hbar }{ m_{ele} \cdot {_{\raise -.3ex 0}c} } } \] | (Lep.Mod.43) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{licht,rot}\;\;\;=\;\;\;\sqrt{ \frac{ 2 \cdot n_{wel} - 1 }{ 2 \cdot n_{wel} } } \cdot \frac{ \hbar }{ m_{ele} \cdot {_{\raise -.3ex 0}c} } } \] | (Lep.Mod.44) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{licht,rot}\;\;\;=\;\;\;\sqrt{ 1 - \frac{ 1 }{ 2 \cdot n_{wel} } } \cdot \frac{ \hbar }{ m_{ele} \cdot {_{\raise -.3ex 0}c} } \;\; , } \] | (Lep.Mod.45) | ||
den wir gleich anschließend für die Berechnung des Lichtrotations-Spins nutzen.
Entsprechend zum Leptonen-Spin in Formel stellen wir die Formel für den Lichtrotations-Spin auf, als Summe des Drehimpulses des Wirkungsquanten-Strings um die Spin-Bahn innerhalb des durch die Lichtbahn geformten Torus:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { s_{lep,licht,rot}\;\;\;=\;\;\;r_{licht,rot} \cdot m_{lep} \cdot c_{licht,rot} } \] | (Lep.Mod.46) |
Mit Hilfe der Formel sowie der Formeln und dann lösen wir dies zu:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}s_{lep,licht,rot}\;\;\;=\;\;\;\\ \qquad\qquad\qquad\qquad \frac{ \sqrt{ 2 \cdot n_{wel} - 1 } }{ n_{wel} } \cdot r_{spin} \cdot m_{lep} \\ \qquad\qquad\qquad\qquad\qquad\qquad\quad \cdot \sqrt{ 2 \cdot n_{wel} - 1 } \cdot c_{spin} } \] | (Lep.Mod.47) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s_{lep,licht,rot}\;\;\;=\;\;\;\frac{ 2 \cdot n_{wel} - 1 }{ n_{wel} } \cdot r_{spin} \cdot m_{lep} \cdot c_{spin} } \] | (Lep.Mod.48) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s_{lep,licht,rot}\;\;\;=\;\;\;\left( 2 - \frac{ 1 }{ n_{wel} } \right) \cdot s_{lep} } \] | (Lep.Mod.49) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s_{lep,licht,rot}\;\;\;=\;\;\;\left( 2 - \frac{ 1 }{ n_{wel} } \right) \cdot \frac{ 1 }{ 2 } \hbar } \] | (Lep.Mod.50) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s_{lep,licht,rot}\;\;\;=\;\;\;\left( 1 - \frac{ 1 }{ 2 \cdot n_{wel} } \right) \cdot \hbar } \] | (Lep.Mod.51) | ||
| ▾ | Der neue, innere Spin steht vermutlich für die Leptonenzahlerhaltung: |
Der mittlere Spin entlang der Lichtbahn um die Spin-Bahn slep,licht,rot, den ich innerer Spin des Leptons nenne, hat nach meiner Vermutung eine ganz besondere Bedeutung.
Entsprechend meinen Vermutungen, dass die Wellenanzahl oder Sternzackenzahl des Leptonen-Strings zur Vermeidung innerer Überschneidungen größer gleich 8, wegen der neutralen elektrischen Ladung der Neutrinos auch durch zwei teilbar sein sollte und wegen des Quark- beziehungsweise Hadronen-Modells möglicherweise auch durch 3 teilbar plausibel ist, kommen wir mindestens auf 8 Wellen oder Sternzacken, möglicherweise gar auf 12, 18 oder noch mehr. Hieraus ergeben sich beispielhaft folgende Werte für den inneren Spin:
Für nwel = 8:
Für nwel = 12:
Dieser gebrochenzahlige Spin ist somit nicht ohne weiteres ein ganzzahlige Vielfaches der Spinquantenzahl \( ½ \). Dazu ist es ein Spin, der nur innerhalb des Torus der Lichtbahn-Spirale um die Spin-Bahn existiert. Räumlich gesehen heben sich die Spins der einzelnen Wirkungsquanten des Strings nämlich auf.
Trotzdem:
Ich vermute, dass, und es ist aus meiner Sicht zu untersuchen, ob und inwieweit, der innere Spin mit der Leptonenzahlerhaltung im Zusammenhang steht.(Verweis: Wikipedia: Leptonenzahl)
Innerer Spin und Quarks (Hadronen)
Welche Rolle der innere Spin in Bezug auf Quarks spielt, ist zu untersuchen.
Was ist in der Physik schon bekannt?
Nach den heutigen Erkenntnissen besitzen die aus Quarks aufgebauten Hadronen alle die Leptonenzahl Null.
Demnach sollten sich die Leptonzahlen der Quarks, insoweit sie eine von Null verschiedene Leptonenzahl besitzen,
innerhalb eines Hadrons zu Null aufsummieren.
Bei Mesonen, die immer aus einem Quark-Antiquark-Paar aufgebaut sind, ist dies wegen der gleich großen
und entgegengesetzten Leptonenzahlen von Teilchen und Antiteilchen der Fall.
Was ergibt sich aus dem Lepton-, Quark- und Hadron-Modell der Quanten-Fluss-Theorie?
In der Quanten-Fluss-Theorie sind Quarks in Hinsicht auf ihre elektrische Ladung \( \pm ⅓ \) oder \( \pm ⅔ \) Leptonen.
In Hinsicht auf ihren Spin jedoch Fermionen mit \( \pm ½ \hbar \).
Insofern ist es spannend, was eine Berechnung des inneren Spins der Quarks ergibt.
Nachfolgen berechnen wir jetzt den Wirkungsquanten-String-Spin um die grüne Lichtbahn slep,wq, also den Spin des Strings innerhalb des spiralförmigen Torus, der die Lichtbahn zentral umhüllt.
Dafür stellen wir wieder mit Hilfe der allgemeinen Wellengleichung die angepasste Wellengleichung der Rotationsgeschwindigkeit vwq,rot der Wirkungsquanten um die grüne Lichtbahn in Abhängigkeit der De-Broglie-Frequenz fele des Leptons und seiner Wellenlänge um die Lichtbahn λwq,rot auf.
Für die De-Broglie-Frequenz fele nutzen wir, wie gehabt, Formel :
Sei die Wellenlänge durch
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \lambda_{wq,rot}\;\;\;=\;\;\;2 \pi \cdot r_{wq,rot} } \] | (Lep.Mod.56) |
gegeben, so können wir die allgemeine Wellengleichung hierauf anpassen mit:
Durch ersetzen der Rotationsfrequenz fele mittels Formel und unsere Interpretation des Pound-Rebka-Snider-Experiments im Rahmen der Quanten-Fluss-Theorie, die zu dem Ergebnis führt, dass die Wirkungsquanten-Rotationsgeschwindigkeit beim kosmischen Beobachter B0 gleich der Lichtgeschwindigkeit 0c ist (siehe Formel ZAF.Wq.31), kommen wir zu
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { v_{wq,rot}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} } \] | (ZAF.Wq.31) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{\raise -.3ex 0}c}\;\;\;=\;\;\;c_{spin} \cdot \frac{ n_{wel} }{ 2 \pi \cdot r_{spin} } \cdot 2 \pi \cdot r_{wq,rot} } \] | (Lep.Mod.59) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{wq,rot}\;\;\;=\;\;\;\frac{ r_{spin} }{ n_{wel} \cdot c_{spin} } \cdot {_{\raise -.3ex 0}c} \;\; . } \] | (Lep.Mod.60) | ||
Hier können wir jetzt die mittle Spin-Geschwindigkeit cspin mit Hilfe von Formel und den mittleren Spin-Radius rspin mit Hilfe von Formel ersetzen
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}r_{wq,rot}\;\;\;=\;\;\;\frac{ r_{spin} }{ n_{wel} \cdot \frac{ {_{\raise -.3ex 0}c} }{ \sqrt{ 2 \cdot n_{wel} } } } \cdot {_{\raise -.3ex 0}c} } \] | (Lep.Mod.61) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{wq,rot}\;\;\;=\;\;\;\frac{ r_{spin} }{ \sqrt{ \frac{ n_{wel}^{2} }{ 2 \cdot n_{wel} } } } } \] | (Lep.Mod.62) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{wq,rot}\;\;\;=\;\;\;\frac{ r_{spin} }{ \sqrt{ \frac{ n_{wel} }{ 2 } } } } \] | (Lep.Mod.63) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{wq,rot}\;\;\;=\;\;\;\sqrt{ \frac{ 2 }{ n_{wel} } } \cdot r_{spin} } \] | (Lep.Mod.64) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{wq,rot}\;\;\;=\;\;\;\sqrt{ \frac{ 2 }{ n_{wel} } } \cdot \sqrt{ \frac{ n_{wel} }{ 2 } } \cdot \frac{ \hbar }{ m_{ele} \cdot {_{\raise -.3ex 0}c} } } \] | (Lep.Mod.65) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}r_{wq,rot}\;\;\;=\;\;\;\frac{ \hbar }{ m_{ele} \cdot {_{\raise -.3ex 0}c} } } \] | (Lep.Mod.66) | ||
und bekommen einen Wirkungsquanten-Rotationsradius, der umgekehrtproportional zur Leptonen-Masse ist.
Die vorstehende Gleichung ist sehr bemerkenswert daher möchte ich ihre Bedeutung in einem kurzen Einschub erläutern. Dieser kann ohne Probleme beim weiteren Verständnis auch zu einem späteren Zeitpunkt gelesen werden.
| ▾ | Träge Masse und starke Wechselwirkung: |
Träge Masse
Die Formel lässt sich zur Masse eines Elementarteilchens mele umformen:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}m_{ele}\;\;\;=\;\;\;\frac{ \hbar }{ r_{wq,rot} \cdot {_{\raise -.3ex 0}c} } } \] | (Lep.Mod.67) |
Dieser Zusammenhang hat die Fähigkeit, die zu erklären, wie Albrecht Giese zeigt. Dies kann sie unter der Bedingung, dass eine Form von Sombrero-Potenzial eine Struktur des Elementarteilchens stabil hält, was wiederum sehr an den Higgs-Mechanismus erinnert.
In der fraktalen Quanten-Fluss-Theorie hält genau ein solches Potenzial die dynamische Struktur der Elementarteilchen-Strings in der Form.
Starke Wechselwirkung
Um die träge Masse aus diesem Zusammenhang zu berechnen benutzt Albrecht Giese die Feldkonstante der starken Wechselwirkung. Dies ist sehr bemerkenswert, weil die String-Spannung beziehungsweise das sogenannte Confinement der Quarks und Gluonen in der fraktalen Quanten-Fluss-Theorie der starken Wechselwirkung entspricht. Das passt plausibel zusammen.
Wir fahren also mit unseren Berechnungen fort:
Entsprechend zum Leptonen-Spin in Formel
stellen wir die Formel für den Wirkungsquanten-String-Spin um die Lichtbahn slep,wq auf, als Summe des Drehimpulses des Wirkungsquanten-Strings
um die Lichtbahn, innerhalb des durch die Wirkungsquanten-String-Schwingung geformten helixförmigen Torus:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { s_{lep,wq}\;\;\;=\;\;\;r_{wq,rot} \cdot m_{lep} \cdot v_{wq,rot} } \] | (Lep.Mod.68) |
Für den Wirkungsquanten-String-Spin um die Lichtbahn ergibt sich dann, unter Zuhilfenahme der Formeln ZAF.Wq.31, für vwq,rot, sowie , für rwq,rot, gefolgt von , für 0c, und dem Vergleich mit
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}s_{lep,wq}\;\;\;=\;\;\;\sqrt{ \frac{ 2 }{ n_{wel} } } \cdot r_{spin} \cdot m_{lep} \cdot {_{\raise -.3ex 0}c} } \] | (Lep.Mod.69) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}s_{lep,wq}\;\;\;=\;\;\;\sqrt{ \frac{ 2 }{ n_{wel} } } \cdot r_{spin} \cdot m_{lep} \cdot \sqrt{ 2 \cdot n_{wel} } \cdot c_{spin} } \] | (Lep.Mod.70) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s_{lep,wq}\;\;\;=\;\;\;2 \cdot r_{spin} \cdot m_{lep} \cdot c_{spin} } \] | (Lep.Mod.71) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s_{lep,wq}\;\;\;=\;\;\;2 \cdot s_{lep} } \] | (Lep.Mod.72) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s_{lep,wq}\;\;\;=\;\;\;2 \cdot \frac{ 1 }{ 2 } \hbar } \] | (Lep.Mod.73) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}s_{lep,wq}\;\;\;=\;\;\;\hbar } \] | (Lep.Mod.74) | ||
zum Spin eines Photons.
Bemerkenswerterweise ist der Wirkungsquanten-String-Spin um die Licht-Bahn tatsächlich der von Photonen, nämlich \( \hbar \). Wir haben es demnach also in ihrer Mechanik mit einer vom Funktionsprinzip her wirklichen Lichtuhr zu tun.
Abschätzung der Richtigkeit der Näherung der Mittelwerte
Sowohl bei der Spin-Geschwindigkeit cspin, als auch beim Spin-Radius rspin handelt es sich um eine Näherung durch Mittelwerte:
Trotz der Schwankung der Spin-Geschwindigkeit ist klar, dass der String nach einem Schwingungsdurchgang ein nwel-tel des Spin-Bahnumfangs zurückgelegt hat. Daher stimmt die Spin-Geschwindigkeit nach einer Schwingung mit ihrem Mittel überein.
Da der String schwingend mal weiter entfernt mal näher dran um die Spin-Bahn rotiert muss sein mittlerer Spin-Radius dem Radius rspin dieser Bahn entsprechen.
XXX XXX XXX XXX XXX
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { c_{licht,rot} } \] | (Lep.Mod.75) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { r_{licht,rot} } \] | (Lep.Mod.76) |
XXX XXX XXX XXX XXX XXX XXX XXX XXX
Berechnung des Neutrino-Modells
XXX XXX Das Neutrino-Modell hat die Besonderheit, dass sich ein Polwechsel des elektrischen Feldes auf zwei Sternzacken verteilt. Daher sind zwei Schwingungsdurchgänge notwendig, um das Modell wieder in einen komplett ununterscheidbaren Zustand zu überführen. Aus der Ferne reicht allerdings ein Durchgang, um diesen Eindruck zu erzeugen, weil die Pole der elektrischen Feldstärke dort ausgleichen. XXX XXX
Berechnung des magnetischen Moments
XXX XXX Siehe Giese … XXX XXX XXX XXX XXX XXX
XXX
XXX XXX XXX XXX XXX XXX XXX XXX XXX
XXX XXX XXX XXX XXX XXX XXX XXX XXX
→
| |
Elektrische Ladung |
|
Variierende Dichten der Wirkungsquanten auf dem Leptonen-String erzeugen elektrische Felder
←
|
Die elektrische Ladung eines Leptons wird durch die unterschiedliche Dichte der Wirkungsquanten auf dem Wirkungsquanten-String und ihre asymmetrische Verteilung und Bewegung im Raum erzeugt (siehe und ). Die elektrische Polarisation schwingt dabei zwischen einem schwachen, der Ladung entgegengesetzen Pol und einem starken, der Ladung entsprechenden Pol.
So ergibt sich im Mittel die elektrische Ladung des Teilchens, ein magnetisches Drehmoment und eine .
Bei den elektrisch neutralen sind die Pole so verteilt, dass die Wellenphasen der String-Struktur immer gleichzeitig beide entgegengesetzten Pole nach außen richten.
→
→ Elektromagnetische Wechselwirkung — Elektroschwache Wechselwirkung
→
| |
Schwache Ladung |
|
Asymmetrisch verteilte Dichten der Wirkungsquanten auf dem Leptonen-String erzeugen schwache Felder
Die schwache Ladung wird durch die unterschiedliche Dichte der Wirkungsquanten auf dem Wirkungsquanten-String und ihre asymmetrische Verteilung und Rotation im Raum erzeugt (siehe ). Dadurch ergibt sich eine asymmetrische, schwingende , die ein magnetisches Drehmoment und eine schwache Ladung zur Folge hat.
→
→
→ Schwache Wechselwirkung — Elektroschwache Wechselwirkung
| |
Masse, Impuls und Energie |
|
Die Wirkungsquanten eines Strings sind die Quanten der Masse, der Energie sowie des Impulses und Ursprung der Quantengravitation
Die Energie eines Elementarteilchens der Quanten-Fluss-Theorie ist schlichtweg proportional zur Anzahl der in seinem Wirkungsquanten-String enthaltenen Wirkungsquanten. Zu sehen ist dies einfach, wenn man die Messung der Energie eines Teilchens auf das Zählen seiner Wirkungsquanten zurück führt.
Dies gilt dann auch ebenso für seine Masse und seinen Impuls:
Die Quantisierung von Masse, Energie und Impuls entspricht in der Quanten-Fluss-Theorie dem Aufbau der Elementarteilchen aus einzelnen Wirkungsquanten; der Messvorgang der Zählung der Wirkungsquanten eines Strings. Die Heisenbergsche Unschärferelation ergibt sich dabei aus einem prinzipiellen Abzählproblem.
Die Abstrahlung der Wirkungsquanten eines Elementarteilchen-Strings ist dabei eng mit der Entstehung der Quantengravitation verbunden.
→ Elementarteilchenmodell
→ Wirkungsquanten — Neue Physik
→ Heisenbergsche Unschärferelation
→ Quantengravitation der Elementarteilchen
| |
Quantengravitation |
|
Wirkungsquanten haben Beugungseffekte in ihrem Umfeld
←
Die Wirkungsquanten eines Leptonen-Strings senden auf ihrer Größenskala Störungswellen in den Raum, welche die Bahnen der Wirkungsquanten von Strings in ihrem Umfeld zu ihnen hin beugen. Die benachbarten Strings wandern so minimal aufeinander zu. Sind viele Strings zu einer großen Masse vereint, so summiert sich dieser Effekt auf. Seine Wirkung ist genau proportional zur Anzahl der Wirkungsquanten der Masse, wie auf der Seite Quantengravitation erklärt wird.
→
| |
Spins |
|
Drei Spins bestimmen die Struktur und Erhaltungssätze der Leptonen
←
| ▾ | Notizen |
(• Die Entwicklung aller Formeln zum Lepton in einem Anhangskapitel unterbringen …)
(• In der Heim-Theorie gibt es Hinweise darauf, wie der Isospin strukturell entsteht und wie sich seine Werte ergeben. Siehe Ordner "Isospin, Spin - Burkhard Heim - Das neue Weltbild des Physikers - cd2v4-07".)
Die drei unterschiedlichen Spins der Leptonen sind (siehe ):
| • |
der bekannte, äußere Spin um das Zentrum (den „Schwerpunkt“), entlang der blauen Spin-Bahn |
| • |
der innere Spin um die Spin-Bahn entlang der grünen Lichtbahn |
| • |
der Wirkungsquanten-Spin um die Lichtbahn |
Alle Spins sind von Masse und Ladung unabhängig. Sowohl der äußere Spin, als auch der Wirkungsquanten-Spin besitzen den von Leptonen bekannten Wert:
|
|
(5.10) |
|
|
(5.69) |
Der innere Spin charakterisiert das Teilchen und sein Wert entspricht seiner wellenförmigen Phase wie folgt:
|
|
(5.37) |
Es gibt in der Natur eine fundamentale Asymmetrie:
Ich vermute, dass die drei Spins in einem Teilchen die Hierarchie äußerer Spin, innerer Spin und Wirkungsquanten-Spin besitzen und fest zueinander ausgerichtet sind. Die feste Ausrichtung ergibt sich, weil sich nach den Beobachtungen ein Teilchen mit seinem immer in einer Paarvernichtung vernichten kann. Dies ist nur möglich, wenn alle Spins des Antiteilchens immer genau entgegengesetzt zu denen des Teilchens sind.
Wie genau diese Spins fest zueinander ausgerichtet sind, das meint jeweils zur darüber liegenden Hierarchieebene links oder rechts herum, ist noch zu klären.
Ich vermute, dass die sich aus der festen Ausrichtung der Spins ergebende Asymmetrie der Urpsrung für die Asymmetrie der ist.
→
| |
Radius |
|
Aufgrund der Struktur des Strings und deren elektroschwachen Felder erscheinen Leptonen nahezu Punktförmig
←
Den Text überarbeiten, er ist etwas komisch und unklar. Die punktförmige Wahrnehmung der Teilchen besser herausarbeiten. Vielleicht das Kapitel in Radien umbenennen …
Die Entwicklung aller Formeln zum Lepton in einem Anhangskapitel unterbringen …
Die rot gefärbten Wirkungsquanten zweier an einer Reaktion beteiligten Elementarteilchen beeinflussen sich im wesentlichen nur
über die Felder, welche sie durch die Struktur ihrer Strings im Raum erzeugen.
Eine direkte Wechselwirkung zwischen ihren Wirkungsquanten findet aufgrund deren geringen Größe und
mangels deren relativ direkten Zusammentreffens kaum statt.
Die durch die elektrisch polarisierten Stellen ihres Strings und deren Bewegung erzeugten
sind bis ins Zentrum ihres punktförmig strukturiert (siehe ).
Da die diesen Feldern entsprechende elektroschwache Wechselwirkung die beobachteten Reaktionen dominiert, erscheinen die Leptonen punktförmig,
obwohl ihr String in Bezug auf die Strukturen der Quantenmechanik eine durchaus relevante Größe besitzt.
Die Formel des Spin-Radius lautet:
|
|
(5.41) |
Der Spin-Durchmesser eines ruhenden Elektrons, mit hypothetischen sechs Phasen, hätte dann die Größe:
|
|
(Lep.77) |
|
|
(Lep.78) |
|
|
(Lep.79) |
|
|
(Lep.80) |
|
|
(Lep.81) |
Hierbei handelt es sich um den mittleren Radius der Wirkungsquanten um den Schwerpunkt des Leptons (blaue Spin-Bahn).
Eine dem nahe kommende, strukturelle Ausdehnung findet sich in The Apparent Mystery of the Electron
des Basisteilchenmodells von Albrecht Giese.
→
→
| |
Antiteilchen |
|
Aus Teilchen kann man nicht durch Drehung oder Spiegelung Antiteilchen machen
Das wesentliche Merkmal von elektrisch geladenen Antiteilchen besteht in ihrer entgegengesetzten Ladung. Bezogen auf die Erläuterungen zur sind die Pole der maximalen und minimalen Dichte der in rot gefärbten Wirkungsquanten vertauscht. Der sowie der eines Teilchens sind bei seinem Antiteilchen in Bezug auf seinen normalen, genau umgekehrt orientiert. Oder die zuletzt genannten Spins bleiben gleich im Raum ausgerichtet und der normale, äußere Spin ist umgekehrt.
Ich folgere, dass es keine einfache Drehung oder Spiegelung im Raum gibt, welche aus einem Teilchen sein Antiteilchen machen könnte oder umgekehrt.
Anti-Neutrinos gleichen also nicht den entsprechenden . Ihre entgegengesetzt verteilten elektrischen Pole würden in der Tat keinen Unterschied machen. Da aber ein Teil ihrer Spins, wie eben erläutert, entgegengesetzt ausgerichtet ist, können beide Teilchen nicht gleich sein.
Dabei ist im Rahmen der Quanten-Fluss-Theorie übrigens zu beachten, dass die heutigen Anti-Neutrinos zu den Teilchen und die Neutrinos zu den Antiteilchen zu zählen sind. Dies ergibt sich aus den beobachteten Teilchenumwandlungen.
→
→
→ Symbolismus — Elektroschwache Wechselwirkung
→ Teilchenumwandlungen — Elektroschwache Wechselwirkung
→
| |
Neutrinos |
|
Das neue Modell offenbart, dass sie sich von ihren Antiteilchen unterscheiden
|
Einen Film erstellen …
Die Neutrinos sind Leptonen. Sie haben eine Struktur, die auch aus sich bewegenden elektrischen Polen besteht, die aber im Mittel elektrisch neutral ist. Aufgrund der asymmetrischen Verteilung und Bewegung der Pole ist allerdings eine vorhanden.
Neutrinos sind nicht gleich ihren Antiteilchen, weil sie sich in der relativen Orientierung ihrer unterscheiden.
Im Rahmen der Quanten-Fluss-Theorie ist zu beachten, dass die heutigen Anti-Neutrinos zu den Teilchen und die Neutrinos zu den Antiteilchen zu zählen sind. Dies ergibt sich aus den beobachteten Teilchenumwandlungen.
→ Neutrinos — Elektroschwache Wechselwirkung
→
→
→
→ Teilchenumwandlungen — Elektroschwache Wechselwirkung
→
| |
Familien und Generationen |
|
Alle Leptonen und sogar auch alle Quarks besitzen den gleichen inneren Spin
Elektron, Myon und Tauon bilden die Familie der und stehen für verschiedene Generationen der gleichen Wirkungsquanten-String-Struktur. Diese Struktur schwingt elektrisch zwischen einen starken elektrischen Hauptpol und einem entgegengesetzten schwachen Nebenpol. So ergibt sich im Mittel der beobachtete elektrische Ladungspol (siehe und Abbildung XXX).
Die -Generationen Elektron-, Myon- und Tauon-Neutrino bilden die Familie der . Auch diese Familie besitzt im Wesentlichen die gleiche Wirkungsquanten-String-Struktur, nur das in diesem Fall positive und negative elektrische Pole gleichzeitig nach außen gerichtet sind (siehe Film XXX Abbildung XXX). Diese Teilchen sind also im Durchschnitt elektrisch neutral, besitzen aber aufgrund der asymmetrischen Verteilung und Bewegung der inneren Pole eine .
Die Generationen der Leptonen unterscheiden sich nur durch ihre energetischen Anregungszustände.
Dies bedeutet, dass ihre Wirkungsquanten-Strings in Ruhe eine unterschiedliche Anzahl an Wirkungsquanten und damit an Energie beziehungsweise Masse beinhalten.
Die beobachteten Teilchenumwandlungen
legen wegen der Erhaltung des inneren Spins(Link) nahe, dass alle Leptonen und sogar ebenfalls alle Quarks
den gleichen Betrag des besitzen.
→
→
→
→ Teilchenumwandlungen — Elektroschwache Wechselwirkung
→ Quarks — Elektroschwache Wechselwirkung
→
| |
Quantenmechanik |
|
Die quantemachanischen Phänomene ergeben sich aus der Struktur der Wirkungsquanten-Strings
Die quantenmechanischen Eigenschaften der Wirkungsquanten-Strings der verschiedenen Elementarteilchen-Familien ergeben sich aus der Struktur ihrer Strings und deren Dynamik. Der Zufall kommt dabei über das „zufällige“ zeitliche und räumliche Zusammentreffen der Komponenten der schwingenden Feinstrucktur zweier oder mehrerer Strings zustande. Dies kommt , weil jeder beteiligte String zur selben Zeit in einem unterschiedlichen Schwingungszustand ist.
Die diskrete Körnigkeit in Form ihrer Wirkungsquanten führt, auf Basis eines prinzipiellen Abzählproblems,
zur bekannten Proportionalität von Energie und Frequenz,
ist aber auch für die Gültigkeit der Heisenbergschen Unschäferelation
verantwortlich.
Die weiteren Phänomene der Quantenmechanik
ergeben sich hingegen aus den unterschiedlichen, der Wirkungsquanten-Strings.
→ Heisenbergsche Unschärferelation
→ Welleneigenschaften der Elementarteilchen — Elementarteilchenmodell
→
→
| |
Welle-Teilchen-Dualismus |
|
Wellen- und Teilchencharakter sind kein Widerspruch
(Beides soll zusammen gebracht worden sein, siehe Coles, »Equivalence of wave–particle duality to entropic uncertainty« und Sekundärliteratur: Lingenhöhl, »Ist die Quantenphysik weniger kompliziert?«
In einem Artikel auf http://www.quantumlah.org/highlight/141220_wave_particle.php ist zu lesen: »›The connection between uncertainty and wave-particle duality comes out very naturally when you consider them as questions about what information you can gain about a system. Our result highlights the power of thinking about physics from the perspective of information,‹ says Wehner, who is now an Associate Professor at QuTech at the Delft University of Technology in the Netherlands.«
Ich hatte schon festgestellt, dass Photonen, also Zirkular polarisierte Elapsonen, Wellen- und Teilcheneigenschaften haben. Welleneigenschaften durch ihre Rotation und Wechselwirkung mit den Vakuum-Elapsonen und Teilcheneigenschaften, weil sie ein zusammen hängendes Gebilde sind.)
In Arbeit…
Das Folgende in die Seiten Welleneigenschaften der Elementarteichen und Vakuum einarbeiten.
In der heutigen Physik kommt die Interpretation der Quantenmechanik im Allgemeinen zu dem Schluss, der Wellen- und der Teilchecharakter der
Elementarteilchen stünden im Widerspruch.
Man meint, diese Sicht entspräche der Heisenbergschen Unschärferelation,
weil nach ihr »Ort und Impuls […] nicht gleichzeitig beliebig exakt bekannt sein«
können.
Nach der Quanten-Fluss-Theorie entspricht die Heisenbergsche Unschärferelation allerdings einem
prinzipiellen Abzählproblem
der Wirkungsquanten des Wirkungsquanten-Strings eines Elementarteilchens; also einer Wahrnehmungsgrenze.
Der scheinbar existenzielle Widerspruch muss folglich nicht in der heute interpretierten Form bestehen bleiben.
Die Quanten-Fluss-Theorie sieht ein Elementarteilchen grob gesprochen als „Wolke“ aus gekoppelten Wirkungsquanten.
Diese kann im Raum „verschmiert“ sein, indem die Wirkungsquanten des Vakuums durch ihr emergentes Verhalten die Wolke
eines virtuellen Elementarteilchens implizieren.
Seine Eigenschaften sind dann im Raum verteilt.
Ein nicht virtuelles, konkretes Elementarteilchen besteht aus einem Wirkungsquanten-String, welcher von einer Wolke aus virtuellen Teilchen umgeben ist.
Es ist also recht klar durch die Kopplung seiner Wirkungsquanten und seine Rotation () auf einen Schwerpunkt konzentriert.
Dabei bringen seine Wirkungsquanten selbst und seine inneren Rotationen die Welleneigenschaften hervor.
Der Übergang vom virtuellen zum konkreten Elementarteilchen und umgekehrt wird durch die Wechselwirkung mit anderen Elementarteilchen vollzogen.
XXX
XXX
XXX
XXX
XXX
XXX XXX XXX XXX XXX XXX XXX
Häufig wird argumentiert, dass der Wellen- und der Teilchencharakter von Elementarteilchen im Widerspruch wären.
Im Grunde trägt aber jeder rotierende Körper den Charakter einer Welle, in Form seiner Rotation, und den eines
Teilchens, in Form der Rotationsachse und seines Schwerpunkts, in sich.
Bei der rotierenden Erde ist der Wellencharakter von außen kaum zu erkennen, da sich für einen Beobachter
vornehmlich nur die Farbe ihrer Oberfläche ändert.
Befindet man sich auf ihrer Oberfläche, so nimmt man ihre Rotation durch die Tag- und Nachtwechsel und die Bewegung
der Sterne schon viel eher wahr.
Befinden sich alledings wesentliche Strukturen eines Teilchens oder Körpers in Rotation, vielleicht sogar um mehrere Achsen, wie beim Leptonen-Modell die , dann kommt der Wellencharakter viel deutlicher zum Vorschein.
→ Welleneigenschaften der Elementarteilchen — Elementarteilchenmodell
→ Heisenbergsche Unschärferelation
| |
Berechnungen |
|
XXX
(• Landé-Faktor/Feinstrukturkonstante: Giese berechnet den Landé-Faktor mit sehr guter Genauigkeit aus seinem Basisteilchenmodell (siehe Giese, The Apparent Mystery of the Electron, Appendix B: The Landé factor.) Soll sich der Landé-Faktor aus der FrQFT ebenso ergeben, dann müssen auch hier immer die zwei gegenüber liegenden Elektronen-String-Segmente einander in ihrer Polarisation addieren. So wie es auch bei der Gravitation geschieht, weil sich die Abstrahlung mit 1/r in den Raum ausbreitet. Seine Herleitung enthält allerdings noch Annahmen, die ich so vielleicht nicht treffen würde. Denn bei ihm wirkt die Kraft (welche ist das genau? String-Spannung oder EM-Polarisation?) eines Basisteilchens nicht nur senkrecht zu seiner Bahn. Ich muss also erst einmal sehen, was die Herleitung der Abflachung der Felder bei mir ergibt! Das elektrische Potential würde zu 1/r passen (vgl. http://de.wikipedia.org/wiki/Elektrisches_Potential).)
XXX XXX XXX XXX XXX XXX XXX XXX XXX XXX XXX XXX XXX XXX XXX XXX XXX
XXX XXX XXX XXX XXX XXX XXX
| |
Fußnoten |
|
| 1. | Der Wirkungsquanten-String schwingt im 3-dimensionalen Bewegungsraum der Quanten-Fluss-Theorie und nicht in vielen Dimensionen, wie ein String der Strintheorie. Durch den Aufbau eines Wirkungsquanten-Strings schwingen allerdings viele seiner Eigenschaften gleichzeitig, die alle auf der Bewegung seiner Struktur in den uns bekannten drei Dimensionen beruhen. Anders als in der Stringtheorie, stehen diese schwingenden Eigenschaften dadurch in enger Abhängigkeit zueinander. Dies hat ein konkretes Modell mit nur wenigen oder gar keinen Freheitsgraden zur Folge. Dadurch liefert die Quanten-Fluss-Theorie eindeutigere Erklärungen und Vorhersagen als die heutige Stringtheorie. | |
| 2. | Acht Phasen oder Sternzacken werden erst einmal hypothetisch angenommen, weil dies die kleinste Anzahl ist, bei der sich im entfalteten Zustand der String innen nicht überschneidet. Neun Phasen sind naheliegend, weil sich dann die Anzahl durch drei teilen lässt, was zu den Drittelladungen des Quarkmodells passt, weil die Quarks als Eindrittel- oder Zweidrittel-Leptonen-Strings modelliert sind. Eine genaue Herleitung der Phasenzahl wird gesucht. Hinweise darauf sind erbeten. | |
| 3. | Vgl. Kiefer, »Auf dem Weg zur Quantengravitation«, S. 37. | |
| 4. |
Vgl. Fließbach, Allgemeine Relativitätstheorie. Vgl. Harrison, Kosmologie, Kap. 8 Allgemeine Relativitätstheorie, S. 253-290. Vgl. Born, Die Relativitätstheorie Einsteins, Kap. VII. Die allgemeine Relativitätstheorie Einsteins, S. 266-324. Vgl. Einstein, »Die Grundlagen der allgemeinen Relativitätstheorie«. Internet: Vgl. Wikipedia, Allgemeine Relativitätstheorie. | |
| 5. | Vgl. Kiefer, »Auf dem Weg zur Quantengravitation«, S. 37. | |
| 6. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 3.1 Grundannahmen zur Raumzeit-Struktur der Elementarteilchen, S. 36-41, hier Alterungspostulat, S. 38. | |
| 7. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 4.1.1 Zeit, Alterung und Licht-Raumzeit-Geometrie, S. 51-56, hier S. 51-52. | |
| 8. |
Vgl. Fließbach, Allgemeine Relativitätstheorie. Vgl. Harrison, Kosmologie, Kap. 8 Allgemeine Relativitätstheorie, S. 253-290. Vgl. Born, Die Relativitätstheorie Einsteins, Kap. VII. Die allgemeine Relativitätstheorie Einsteins, S. 266-324. Vgl. Einstein, »Die Grundlagen der allgemeinen Relativitätstheorie«. Internet: Vgl. Wikipedia, Allgemeine Relativitätstheorie. | |
| 9. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 4.1.1 Zeit, Alterung und Licht-Raumzeit-Geometrie, S. 51-56, hier S. 52. | |
| 10. |
Vgl. Fließbach, Allgemeine Relativitätstheorie, Teil II Spezielle Relativitätstheorie, S. 7-38. Vgl. Born, Die Relativitätstheorie Einsteins, Kap. VI. Das spezielle Einsteinsche Relativitätsprinzip, 194-266. Vgl. Einstein, »Zur Elektrodynamik bewegter Körper«. Internet: Vgl. Max Planck Institute for Gravitational Physics, »Spezielle Relativitätstheorie«. Vgl. Wikipedia, Spezielle Relativitätstheorie. | |
| 11. |
(Primärliteratur einfügen!) Internet: Vgl. Max Planck Institute for Gravitational Physics, »Ruhemasse«. Vgl. Wikipedia, Masse, Spezielle Relativitätstheorie, Ruhemasse. | |
| 12. |
(Weitere Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Materiewelle. | |
| 13. |
Vgl. Einstein, »Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?«. Internet: Vgl. Wikipedia, Äquivalenz von Masse und Energie. | |
| 14. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Quantenphysik. | |
| 15. |
Dies ist eine Korrektur gegenüber meiner Arbeit von 2012, wo die Annahme war, dass der Wirkungsquanten-String, dort noch Gravitonen-String genannt, zwei Mal um die Licht-Bahn rotiert, während er ein Mal um die Spin-Bahn rotiert: Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 5 Qualitative Physik der QM und ART, 5.2 Elementarteilchen und ihre Wechselwirkungen, 5.2.1 Leptonen, S. 89-100, hier S. 95. | |
| 16. |
Vgl. Fließbach, Allgemeine Relativitätstheorie, Teil III Physikalische Grundlagen der ART, Kap. 12 Gravitationsrotverschiebung, S. 58-64. Vgl. Vessot, »Test of Relativistic Gravitation with Maser«. Vgl. Pound, »Effect of Gravity on Gamma Radiation«. Internet: Vgl. Wikipedia, Pound-Rebka-Experiment. | |
| 17. | Vgl. Giese, The Origin of Mass, Kap. 1 Summery, S. 1 — Kap. 2 The Fundamental Mechanism of Inertial Mass — Kap. 3 Quantitative Determination of the Mass of an Elementary Particle, S. 2–6. | |
| 18. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Higgs-Mechanismus. | |
| 19. |
(Primärliteratur einfügen!) Sekundärliteratur: Vgl. Ent, »Der Klebstoff der Welt«. Internet: Vgl. Wikipedia, Starke Wechselwirkung. | |
| 20. | Vgl. Giese, The Origin of Mass, Kap. 3 Quantitative Determination of the Mass of an Elementary Particle, S. 3–6, hier S. 3. | |
| 21. |
(Primärliteratur einfügen!) Sekundärliteratur: Vgl. Ent, »Der Klebstoff der Welt«, S. 60, 61. Internet: Vgl. Wikipedia, Confinement. Vgl. Alkofer, Quark Confinement (Online), S. 1. | |
| 22. |
Dies ist eine Korrektur gegenüber meiner Arbeit von 2012, wo die Annahme war, dass der Wirkungsquanten-String, dort noch Gravitonen-String genannt, zwei Mal um die Licht-Bahn rotiert, während er ein Mal um die Spin-Bahn rotiert: Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 5 Qualitative Physik der QM und ART, 5.2 Elementarteilchen und ihre Wechselwirkungen, 5.2.1 Leptonen, S. 89-100, hier S. 95-96. | |
| 23. |
Vgl. Wikipedia, Lepton. Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 5.2.1 Leptonen, S. 89-100, hier S. 92. | |
| 24. |
Im nachfolgenden Verweis wird der Spin aufgrund eines Irrtums noch auf ½ℏ berechnet. Die aktuelle Berechnung ist aber noch nicht im Netz veröffentlicht. Es soll hier ein separatee Kapitel mit den Berechnungen erstellt werden: Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 5.2.1 Leptonen, S. 89-100, hier S. 96. Dort wird slep,wq noch als slep,gr bezeichnet. | |
| 25. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 5.2.1 Leptonen, S. 89-100, hier S. 94. Dort wird nphase noch als npol bezeichnet. | |
| 26. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 5.2.1 Leptonen, S. 89-100, hier S. 94. Dort wird nphase noch als npol bezeichnet. | |
| 27. | Vgl. NIST, CODATA Value: electron Mass. | |
| 28. | Vgl. NIST, CODATA Value: Planck constant over 2 pi. | |
| 29. | Vgl. NIST, CODATA Value: speed of light in vacuum. | |
| 30. | Vgl. Giese, The Apparent Mystery of the Electron, Kap. 2.2.1 The Basic Calculation, S. 2-3, hier S. 3. | |
| 31. |
Vgl. Fritzsch, Mikrokosmos, 7. Kap. Oszillierende Neutrinos, S. 119-127. Vgl. Wikipedia, Neutrino. | |
| 32. | Wilczek, Das rätselhafte Elektron. | |
| 33. | Auch in der Stringtheorie können Strings durch emergentes Verhalten andere Strings implizieren. Vgl. Brian Green heraussuchen. |
| |
Stand 29. Februar 2024, 17:00 CET.
-
Permanente Links:
(Klicke auf die Archivlogos
zum Abruf und Ansehen
der Archive dieser Seite.) -

-
archive.todaywebpage capture