Einleitung
Die Erweiterung der Ordinalzahlen zu einem Ring
Negative Ordinalzahlen und Vorgänger aller Limeszahlen
| ▾ | Notizen |
Offene Fragestellungen
• Ist \( 2^{ω} \) eine Ordinalzahl und wenn ja, wo ordnet sie sich in den Ordinalzahlen ein?
– Diese Fragestellung taucht auf der Seite Die arithmetische Struktur der Geometrie auf.
– Kann dabei die Gleichung \( ω = 2 \cdot 3 \cdot 5 \cdot 7 \cdot 11 \cdot 13 \cdot \cdots \), aus dem Beweis der Primzahlprodukt-Vermutung, helfen?
– Denn klar ist, dass \( 2^{ω} \!< ω^{ω} \) sein muss.
– Aber gilt für jedes \( n \in \mathbb{N} \), dass \( ω^{n} \!< 2^{ω} \!< ω^{ω} \) ist?
– Siehe Wikipedia: Ordinalzahl, Rechenoperationen und Wikipedia: Transfinite Arithmetik
Ausgangspunkt der Biordinalzahlen sind die Ordinalzahlen. Bei den Elementen der Menge der Ordinalzahlen \( \mathbb{On} \) handelt es sich um die Fortsetzung des Zählens oder der uns allgemein bekannten Anzahl von Dingen ins Aktual-Unendliche.
Die nachfolgend eingeführten Biordinalzahlen erweitern das Zählen (Vorwärtszählen) um das Rückwärtszählen von jeder Zahl aus bis in den negativen Bereich. Das bedeutet, dass das Rückwärtszählen und die Subtraktion innerhalb der Biordinalzahlen vollständig definiert sind, was innerhalb der Ordinalzahlen nicht der Fall ist.
Die Elemente der Menge der Biordinalzahlen \( \mathbb{Bn} \) definieren so nicht nur die Anzahlen, die vorhanden sind, sondern auch die Anzahlen, die an etwas vollständigem Fehlen, wie wir sehen werden. Durch die Erweiterung werden die Ordinalzahlen als Biordinalzahlen zu einem algebraischen Ring. Denn nun sind in den Biordinalzahlen die Addition und vollständige Subtraktion und ihr neutrales Element „Null“ sowie auch die Multiplikation und ihr neutrales Element „Eins“ definiert.
Erreichte und erwartete Erkenntnisgewinne
Aus der Perspektive der Superial-Zahlen bringt dies auch ein besseres Verständnis der positiven aktual unendlichen Zahlen, wie zum Beispiel \( \s - 1 \), mit sich. Denn hier fehlt an \( \s \) etwas.
Auch zum Beweis der Primzahlprodukt-Vermutung trägt die mengentheoretische Perspektive des Negativen tiefe Einsichten bei, indem festgestellt wird, dass \( ω - 1 \) zu einer riesigen Lücke zwischen den endlichen natürlichen Zahlen und dem hier nachgewiesenen Produkt aller endlichen Primzahlen \( ω \) gehört.
Und nicht zuletzt können wir im Zusammenhang mit geometrischen Überlegungen etwas über die ontologische Struktur des Zählens lernen, deren Erweiterung auf das Negative eine grundlegende Asymmetrie in den ganzen Zahlen erkennen lässt. Meine Intuition sagt mir, dass diese Asymmetrie gemeinsam mit der bewiesenen Primzahlprodukt-Vermutung in der Lage sein könnte entscheidendes zur Klärung der Riemannschen Vermutung beizutragen.
Ordinalzahlen
Dabei werden zunächst die natürlichen Zahlen durch eine Entsprechung zu eineindeutig bestimmten Mengen dargestellt, die selber genau eine Anzahl an Mengen enthalten, wie die jeweilige natürliche Zahl besagt.
Die Ordinalzahlen sind so über ihre Definition durch geordnete Mengen folgendermaßen bestimmt:
Deshalb soll gelten, dass die Null ein Element der natürlichen Zahlen ist, wie in den Peano-Axiomen zur Definition von \( \mathbb{N} \) gefordert und wie für angeordnete Körper definiert:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \mathbb{N}\;\;\;≔\;\;\;\mathbb{N}_{0} } \] | (BO.Ein.8) |
Der Übergang vom Endlichen ins Aktual-Unendliche geschieht durch die Feststellung, dass dann auch die Anzahl der Elemente der Menge der natürlichen Zahlen \( \mathbb{N} \) durch ein Symbol dargestellt werden kann, nämlich \( ω \); und nach Formel so dann auch \( ω + 1 \) und folgende:
Insgesamt sehen wir, dass jede definierte Zahl der Anzahl der Elemente in einer eineindeutig bestimmten geordnete Menge entspricht.
Die Anzahl \( ω \) symbolisiert mathematisch gesehen die aktual unendliche Anzahl, die den Schritten einer vollständigen Induktion entspricht, um alle endlichen Zahlen von der Null an vollständig durchzuzählen.
Grundsätzliche Idee zur Erweiterung der Ordinalzahlen ins Negative
Der Ansatz vorerst beispielhaft mit der Menge der natürlichen Zahlen \( \mathbb{N} \), zum einfachen Einstieg und erweiterten Verständnis
Aufgrund meines strukturellen Interesses an der Unendlichkeit und meiner Neugier suchte ich vor vielen Jahren nach einer möglichen Fortsetzung der Ordinalzahlen ins Negative. Schließlich kam ich darauf, dass negative Zahlen zum Beispiel über das Fehlen von bestimmten Mengen an der Menge der natürlichen Zahlen dargestellt werden können:
Auch hier wird konsequenterweise das Prinzip aufrecht erhalten, dass die Menge, die eine Zahl repräsentiert in Richtung des Negativen in ihrer Anzahl sinkt. An einer gegebenen Anzahl fehlen entsprechend viele Zahlen.
Der Ansatz mit der Menge der natürlichen Zahlen \( \mathbb{N} \) trägt nur bedingt
Wollen wir die Ordinalzahlen um jede Form von Subtraktion erweitern, dann ist der Ansatz mit \( \mathbb{N} \) nicht ausreichend:
Zum einen bedeutet unser gewünschtes Ziel auch von \( ω \) aus rückwärts zu zählen, ohne, dass dies direkt negative Zahlen ergibt. Doch dies entspricht im Grunde genau der zuvor genannten beispielhaften Idee, die Ordinalzahlen ins Negative zu erweitern, wie wir nachfolgend sehen werden. Zum anderen ist es so, dass wir über das zuvor genannte Beispiel quasi am „Ende“ des Ins-Negative-Zählens wieder bei der leeren Menge landen, also bei der Null, was einen Zirkel ergibt, der so nicht sinnvoll ist, weil er das negative „Ende“ der ganzen Zahl mit der Mitte ihrer Zahlengeraden verbindet.
Beides kann vermieden werden, wenn wir anstatt \( \mathbb{N} \) das Mengenuniversum \( \mathbb{U} \) zur Definition der negativen Zahlen verwenden: Wir können \( \mathbb{N} \) als \( ω \) benutzen, um von dort aus rückwärts zu zählen. Und da \( \mathbb{U} \) nicht nur die Ordinalzahlen enthält, sondern alle Mengen, landen wir nicht bei der leeren Menge, wenn wir endlos rückwärts ins Negative zählen, denn es bleiben alle anderen Mengen, die nicht den Ordinalzahlen entsprechen, übrig.
Biordinalzahlen als Erweiterung der Ordinalzahlen
Der Ansatz mit dem Mengenuniversum \( \mathbb{U} \) zur allgemeinen Definition der Subtraktion von Ordinalzahlen
Auch, wenn sich auf die oben geschilderte Weise endliche negative Zahlen sinnvoll darstellen lassen, können wir so nicht alle negativen Ordinalzahlen darstellen. Die Darstellung von \( –ω \) entspräche wie gesagt dann der leeren Menge, die aber schon der Null entspricht. Noch größere unendliche negative Ordinalzahlen lassen sich so generell nicht darstellen, denn an der Menge der natürlichen Zahlen \( \mathbb{N} \) können nicht mehr Zahlen fehlen, als drinne sind.
Negative Ordinalzahlen
Die Lösung dieses Problems finden wir, wie gesagt, darin, anstatt Zahlen an der Menge der natürlichen Zahlen fehlen zu lassen,
sie aus dem Mengenuniversum zu entfernen.
Das Mengenuniversum \( \mathbb{U} \) ist die kleinste Klasse von Mengen, die alle Mengen enthält, die definierbar sind. Am Mengenuniversum können wir quasi beliebig viele Zahlen fehlen lassen, wenn wir diese alle durch Mengen darstellen. Wir ersetzen also die Menge der natürlichen Zahlen \( \mathbb{N} \) in unserer oben geschilderten Idee durch das Mengenuniversum \( \mathbb{U} \):
Auch in diesem Fall wird konsequenterweise das Prinzip aufrecht erhalten, dass die Klasse – das Mengenuniversum ist auch ein Container, aber definitionsgemäß keine Menge, sondern eine Klasse –, die eine Zahl repräsentiert zum Negativen hin in ihrer Anzahl sinkt.
Erweiterung der Limeszahlen um ihre Vorgänger
Wir möchten ja erreichen, dass wir innerhalb der Biordinalzahlen generell von jeder Zahl aus nicht nur in die positive Richtung,
sondern auch in die negative Richtung zählen, also die Vorgänger benennen, können.
Die sogenannten Limeszahlen,
wie \( ω \), \( 2 ω \) oder \( ω^{2} \), haben in unserer Konstruktion immer noch keine Vorgänger.
Die Vorgänger der Limeszahlen lassen sich nun entsprechend der absolut negativen Zahlen definieren:
Diese Definition, basierend auf \( \mathbb{N} \), wurde eingangs für die Definition der absolut negativen Zahlen in Erwägung gezogen, dafür jedoch wieder verworfen, und bekommt hiermit ihre passende Rolle.
Herleitung des Ansatzes der allgemeinen Subtraktion mit positivem Ergebnis
Aber wie steht es mit der Eindeutigkeit, der Praktikabilität und der generellen Plausibilität in komplizierteren Fällen?
An folgendem Beispiel können wir einmal sehen, worum es geht:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { ω^2 - ω - n\;\;\;=\;\;\;ω^2 - \left( ω + n \right) } \] | (BO.Ein.29) |
Diese beiden Darstellungen sind aus Sicht der an \( ω^{2} \) fehlenden Mengen im ersten Moment nicht identisch. Dabei müssen wir uns zuerst klar machen, dass an \( ω^{2} \) auch nur die Mengen fehlen können, die enthalten sind.
So taucht die Frage auf, ob es nicht generell möglich ist, immer die folgende Definition zu benutzen, wenn \( \lambda \) die größte Limeszahl in der Summe ist und \( \beta \) die restlichen Summanden kleinerer Limeszahlen zusammenfasst:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \lambda - \beta\;\;\;≔\;\;\;\lambda \setminus \beta } \] | (BO.Ein.30) |
Dann wäre das Beispiel so definiert:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { ω^2 - \left( ω + n \right)\;\;\;≔\;\;\;ω^2 \setminus \left( ω + n \right) } \] | (BO.Ein.31) |
Und das erscheint schlüssig, weil alle Zahlen, die aus \( ω^{2} \) entfernt werden auch darin enthalten sind.
Doch was wäre, wenn sich Vorzeichen der hinteren Summanden ändern:
Das scheint auch schlüssig zu sein, weil möglich, denn die weggelassenen Mengen existieren in \( ω^{2} \) beziehungsweise in \( ω \), als auch eineindeutig, denn es gibt keine andere Möglichkeit, die selbe Darstellung des Wertes durch eine solche Konstruktion zu erreichen.
Und diese Darstellung erfüllt auch die wichtige Eigenschaft, dass die durch Mengen dargestellte Zahl die Anzahl an Mengen enthält, wie ihr Wert groß ist, oder diese Anzahl aus der Klasse aller Mengen entfernt wird. Am vorstehenden Beispiel veranschaulicht bedeutet dies: Beim Wert \( ω^{2} – ω + n \) haben wir als Basis die Menge \( ω^{2} \) aus der wir die Mengen in \( ω \) herausnehmen, die Mengen in \( n \) jedoch drinnen belassen beziehungsweise wieder hinzufügen:
Entsprechendes gilt auch für alle anderen Vorgänger aller Limeszahlen.
Auf diese Weise entsteht das von einer Limeszahl aus Rückwärtszählen und dann auch wieder von dort aus in kleineren Schritten vorwärtszählen durch unterschiedliche Kombinationen des Entfernens von in ihr enthaltenen Mengen. Es entstehen hierdurch innerhalb der Menge der Basis-Limeszahl keine Mengen, die von ganz neuer Struktur sind. Sondern es ändern sich wirklich nur die Mengenkombinationen in der obersten Ebene der größten Limeszahl. Alle tieferen Ebenen bleiben unberührt.
Die Menge der Biordinalzahlen \( \mathbb{Bn} \)
Die Menge der Ordinalzahlen, erweitert, um die neuen subtraktiven Möglichkeiten, ergeben die neue Menge der Biordinalzahlen \( \mathbb{Bn} \).
| ▾ | Verworfene Möglichkeiten: |
Umgekehrte Klammerung
Überprüfen
• Warum sollte die Addition von \( n \) in \( (ω^{2} – ω) + n \) anders laufen als oben?
Die andere Möglichkeit ist, wir klammern von vorne:
Dann würden wir von \( ω^{2} – ω \) um \( n \) Schritte neu loszählen und erhielten so bisher nicht da gewesene Mengen, die diese Zahlen darstellten. Das finde ich viel weniger intuitiv, weil sich die Strukturen der Mengen dann nicht nur in der obersten Verschachtelungsebene der größten Limeszahl ändern, sondern auch in tieferen Ebenen.
Noch komplexer wird es dann im folgenden Beispiel:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { ω^3 - \left( ω^2 - \left( ω - n \right) \right)\;\;\;=\;\;\;\left( \left( ω^3 - ω^2 \right) + ω \right) - n } \] | (BO.Ein.40) |
So ergibt sich in dieser Möglichkeit ein heilloses Durcheinander.
Deshalb ist für mich diese Möglichkeit zu verwerfen, wenn wir oben eine wunderbar einfache Möglichkeit gefunden haben, dasselbe sehr übersichtlich und plausibel zu leisten.
Entfernen der (nur einer) Menge mit den Zahlen vom Mengenuniversum
Eine noch ganz andere Möglichkeit, die ich in meiner Abhandlung über Biordinalzahlen gewählt hatte und jetzt verworfen habe, ist, wir entfernen nicht den Mengeninhalt einer zu subtrahierenden Zahl vom Mengenuniversum \( \mathbb{U} \) (siehe ), sondern die Zahl selber:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \lambda - \beta\;\;\;≔\;\;\;\lambda \setminus \left\{ \beta \right\} } \] | (BO.Ein.41) |
Diese Variante hat das Verhalten, dass sich die Anzahl der Mengen in einer Limeszahl oder im Mengenuniversum nicht verändert, weil immer nur eine Menge entfernt wird. Im Gegensatz dazu werden in der Variante oben, für die wir uns entschieden haben, immer so viele Mengen entfernt, wie die Größe (Anzahl) der zu subtrahierenden Zahl ist. Die Anzahl der verbleibenden Mengen entspricht also der Zahl, die dargestellt werden soll.
Die obere Variante erfüllt unser Ziel, jede Zahl durch eine Menge darzustellen, die die Anzahl von Mengen enthält, die der Zahl selber gleich ist. Daher haben wir uns für die obige Variante entschieden und nicht für die hier erläuterte.
→
Integrierte Mengenlehre |
 |
Erweiterung der Mengenlehre durch Antimengen auf das integrierte Mengenuniversum
Um wohldefiniert mit Biordinalzahlen mit der uns bekannten Mengenlehre(Verweis) arbeiten zu können bedarf es einer Definition, mit was für Objekten wir es hier zu tun haben und einer Erweiterung der Mengenlehre auf all diese Objekte.
Wenn wir negative Zahlen, wie oben, durch das Fehlen von Mengen an der Klasse(Verweis) des Mengenuniversums \( \mathbb{U} \) definieren, dann bedeutet dies, dass wir das Universum der „normalen“ Mengen verlassen. Denn die Klasse des Mengenuniversums, an der unterschiedliche Kombinationen an Mengen fehlen, sind selber auch keine Mengen, sondern ebenfalls Klassen.
Wir können allerdings sagen, dass es sich hierbei um eine besondere Klasse von Klassen handelt: Wir nennen nun eine Klasse, bei der am Mengenuniversum alle Mengen in einer nicht leeren Menge \( a \) fehlen, ihre Antimenge \( a^– \). Ebenso nennen wir die Klasse, die alle Antimengen enthält, das Antimengenuniversum \( \mathbb{U}^- \). Zuletzt nennen wir die Klasse, die alle Mengen sowie alle Antimengen enthält das integrierte Mengenuniversum \( \mathbb{U}^i \).
Sei, abgeleitet von Formel ,
die Definition der Antimenge zu jeder Menge \( a \), die nicht leer ist. Es existiert dabei keine Definition der Antimenge zur leeren Menge:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( a = \varnothing \right) \left[\; \nexists a^{-} \;\right] } \] | (BO.Ein.IM.2) |
Die leere Menge ist hier ausgeschlossen, weil ihre Antimenge das Mengenuniversum \( \mathbb{U} \) selber wäre, was zu einem Widerspruch führen würde, den wir gleich noch herausarbeiten. Für die leere Menge ist also keine Antimenge definiert.
So ergibt sich
als Definition des Antimengenuniversums.
Das Mengenuniversum und das Antimengenuniversum überschneiden sich nicht
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \mathbb{U} \cap \mathbb{U}^{-}\;\;\;=\;\;\;\left\{ \right\} } \] | (BO.Ein.IM.4) |
und beide zusammen
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \mathbb{U}^{i}\;\;\;≔\;\;\;\mathbb{U} \cup \mathbb{U}^{-} } \] | (BO.Ein.IM.5) |
ergeben das integrierte Mengenuniversum.
Hier sehen wir auch, dass, ohne Ausschluss der leeren Menge bei der Definition der Antimengen (siehe Formel ), das Antimengenuniversum \( \mathbb{U}^{–} \) widersprüchlicher Weise das Mengenuniversum \( \mathbb{U} \) enthalten würde, obwohl sich beide zum integrierten Mengenuniversum \( \mathbb{U}^{i} \) ergänzen sollen.
So können wir jetzt eine allgemeine Definition der Negierung von integrierten Mengen angeben.
Für die Negation einer integrierten Menge gilt also:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall a \in \mathbb{U}^{i} \right) \left[ -a\;\;\;=\;\;\;\begin{cases} a^{-} & \text{ falls } a \in \mathbb{U} \setminus \left\{ \varnothing \right\} \\ a & \text{ falls } a = \varnothing \\ \mathbb{U} \setminus a & \text{ falls } a \in \mathbb{U}^{-} \end{cases} \right] } \] | (BO.Ein.IM.6) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\left( \forall a \in \mathbb{U}^{i} \right) \left[ -a\;\;\;=\;\;\;\begin{cases} a & \text{ falls } a = \varnothing \\ \mathbb{U} \setminus a & \text{ falls } a \in \mathbb{U}^{i} \setminus \left\{ \varnothing \right\} \end{cases} \right] } \] | (BO.Ein.IM.7) | ||
Alle negierten integrierten Mengen sind wieder integrierte Mengen:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall a \in \mathbb{U}^{i} \right) \left[\; -a \in \mathbb{U}^{i} \;\right] } \] | (BO.Ein.IM.8) |
(In Arbeit …)
(In Arbeit …)
→
| |
Ontologische Deutung |
|
Was wir wohl nicht sehen
←
Was geht beim Arbeiten mit Mengen implizit vor sich, was wir wohl nicht sehen, was uns nicht bewusst ist?
Wir wollen dies hier vor allem ontologisch betrachten, also die Lehre von Seienden betreffend.(Verweis) Seiend auch besonders im Sinne von Struktur und hier von verborgener Struktur.
Ontologische Funktion unseres Fokus
Der Auswahldualismus oder Bewusstseinsdualismus
Die vorgestellte Methode zur Darstellung negativer Zahlen durch Mengen oder besser gesagt durch macht deutlich, dass eine Menge eine Auswahl aus den Möglichkeiten und eine Antimenge beziehungsweise negative Menge die Nichtauswahl aus den Möglichkeiten darstellt. Bei der Nichtauswahl aus den Möglichkeiten bleiben dann alle anderen Möglichkeiten ausgewählt. Symbolisch wird durch die Klammer, die etwas enthält, eine Auswahl getroffen, die diese vom Rest der Auswahlmöglichkeiten abgrenzt, die Auswahl umhüllt.
Implizit haben wir es oben also immer mit der Menge der natürliche Zahlen \( \mathbb{N} \) zu tun. Die Auswahl befindet sich in der Menge- oder Auswahl-Klammer oder Auswahl-Hülle und der Rest unsichtbar außerhalb dieser. Unsere Betrachtung behandelt also immer die Menge \( \mathbb{N} \), die in zwei Teile zerlegt ist: Einen Teil, auf den wir fokussierten – der bewusste Teil – und einen Teil, den wir ausblenden – der unbewusste Teil. Naturphilosophisch gesehen, haben wir es mit einem Dualismus beziehungsweise einer Polarität zu tun, dem Auswahldualismus oder Bewusstseinsdualismus.
Noch näher betrachtet handelt es sich beim Auswahl- oder Bewusstseinsdualismus um einen fraktalen Dualismus. Denn zunächst wählen wir die Menge \( \mathbb{N} \), nehmen sie in unseren Fokus und blenden damit alles andere was existiert aus. Anschließend gehen wir in diese Menge und wählen in ihr wieder einen Teil aus, den wir nun in den näheren Fokus nehmen und damit alle anderen Elemente in \( \mathbb{N} \) ausblenden. Wir haben dann also schon vier Fraktalebenen: Alles was existiert, darin die Menge \( \mathbb{N} \), darin alle Elemente in dieser Menge und dann darin die Teilmenge der Elemente, die wir letztendlich aus den Elementen in \( \mathbb{N} \) ausgewählt haben.
Eine Invertierung oder Vertauschung des Fokus auf die bewussten und unbewussten Elemente aller beteiligten Ebenen nutzen wir nun zur Darstellung negativer Zahlen.
Wählen wir eine einzige Ordinalzahl, beispielsweise die \( 2 \), dann läuft dies in folgenden Schritten auf diesen Ebenen ab:
Dann fokussieren wir uns eigentlich auf eine Auswahl-Menge, die die ausgewählte Zahl enthält, hier durch zwei neue Klammern mit Pfeilen nach innen symbolisiert:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \lSelSet 2 \rSelSet\;\;\;=\;\;\;\lSelSet \left\{ 0, 1 \right\} \rSelSet } \] | (BO.Ein.OD.4) |
Um die Menge mit unserer Auswahl aus \( \mathbb{N} \) herum befinden sich ja implizit alle Zahlen, die wir nicht aus \( \mathbb{N} \) ausgewählt haben, denn wir haben ja zum Ausdruck gebracht, dass wir uns mit den Elementen in \( \mathbb{N} \) beschäftigen:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \lSelSet 2 \rSelSet\;\;\;=\;\;\;\lSelSet \left\{ \lSelSet 0, 1 \rSelSet , 2, 3, 4, 5, \cdots \right\} \rSelSet } \] | (BO.Ein.OD.5) |
Und dort existieren natürlich auch alle restlichen Mengen, die es in \( \mathbb{U} \) noch gibt:
Wenn wir unseren Fokus von der \( 2 \) zu allen anderen wechseln, dann sollte dies \( -2 \) ergeben, denn die \( 2 \) fehlt ja nun, und sieht folgendermaßen aus
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \lSelSet \! - \! 2 \rSelSet\;\;\;=\;\;\;\lSelSet \lSelSet \left\{ \rSelSet 0, 1, \lSelSet 2, 3, 4, 5, \cdots \right\} \rSelSet \cup \left( \mathbb{U} \setminus \mathbb{N} \right) \rSelSet } \] | (BO.Ein.OD.7) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\lSelSet \! - \! 2 \rSelSet\;\;\;=\;\;\;\lSelSet \lSelSet \left\{ 2, 3, 4, 5, \cdots \right\} \rSelSet \cup \left( \mathbb{U} \setminus \mathbb{N} \right) \rSelSet } \] | (BO.Ein.OD.8) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\lSelSet \! - \! 2 \rSelSet\;\;\;=\;\;\;\lSelSet \mathbb{U} \setminus \left\{ 0, 1 \right\} \rSelSet } \] | (BO.Ein.OD.9) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\lSelSet \! - \! 2 \rSelSet\;\;\;=\;\;\;\lSelSet \mathbb{U} \setminus 2 \rSelSet } \] | (BO.Ein.OD.10) | ||
was zu zeigen war.
Wir sehen hieran, dass die Berücksichtigung des impliziten beziehungsweise unbewussten Vorgehens beim Fokussierungsprozess verdeutlicht, was eigentlich im „Verborgenen“ vor sich geht. Der fraktale Auswahl- oder Bewusstseinsdualismus hilft uns, dies zu verstehen, und zeigt, dass die gewählte Darstellung der negativen Zahlen durch Antimengen eine bedeutende Beziehung zum Realen hat, also zu realen Vorgängen im Verborgenen.
Die Zuordnung der Werte zur ontologischen Struktur führt zu einer naturphilosophisch sehr interessanten , die wir später näher betrachten werden.
Ontologische Aussagenlogik
In Bezug auf negative Zahlen führt die Vorstellung generell zur Verwirrung, dass die Null ja das Nichts repräsentiert, und negative Zahlen dann ja noch weniger als das Nichts wären. So etwas könne es doch nicht geben, denken wir spontan, und ich meine auch begründet. Ontologisch, also vom Seienden aus, betrachtet kann es nicht weniger geben, als das es nichts gibt.
Was wir nicht so einfach bemerken, salopp formuliert, nicht auf der Reihe haben, ist, dass es immer implizit um das Meer der Möglichkeiten geht, aus denen wir etwas auswählen. Auf Aussagenlogik bezogen und am Beispiel von Mengen ausgedrückt, sind die leere Menge und alle Möglichkeiten sehr nahe beieinander liegend.
Denn haben wir alle Möglichkeiten gleichwertig, dann können wir uns nicht für eine entscheiden, weil keine zur Auswahl heraussticht. Das erscheint so gesehen sehr ähnlich, als hätten wir keine Möglichkeit.
Vergleichbar ist auch die folgende Aussage:
Wem gehört das Wissen der Welt?
Allen und damit keinem.
Aus dieser Perspektive ist ›allen‹ und ›keinem‹ im Grunde identisch, weil es um die Differenz der Besitzenden untereinander geht, die in beiden Fällen gleich ist.
In beiden Fällen geht es quasi um ein „Kräftegleichgewicht“, dass zu einer Entscheidung führen kann. Alle Möglichkeiten zu haben, ist vollständige Harmonie und ein Ausgleich der „Kräfte“, ebenso wie keine Möglichkeiten zu haben.
In der Konstruktion der Zahlen gibt es aber einen Unterschied, denn wir wollen Eindeutigkeit. Und alle Möglichkeiten nutzen wir schon dazu, den Rahmen der Dinge zu bestimmen, von denen wir ausgehen, dass sie möglich sind. So bleibt nur die leere Menge, um auszudrücken, dass die Auswahlmöglichkeiten ausgeglichen sind.
Aber wir haben, ausgehend von beiden gleichwertigen Gleichgewichten, auf diese Weise zwei Möglichkeiten eine Auswahl zu bestimmen: Ein Mal, indem wir aus allen Möglichkeiten „wenige“ auswählen, und ein Mal, indem wir aus allen Möglichkeiten „wenige“ weglassen und damit den Rest auswählen. Beides macht einen erheblichen Unterschied und versetzt uns in die Lage, plausibel und logisch sinnvoll Gewähltes als Positives und Weggelassenes als Negatives zu differenzieren.
Ontologie der Polarität
Polarität bringt etwas zur Existenz und zur Wirkung
Durch die Auswahl oder das Weglassen von Dingen aus allen Möglichkeiten entsteht eine Polarität, die etwas zur stabilen Existenz bringt. Es ist ein Symmetriebruch, der die neutrale Harmonie stört, der zu „Kräften“ führt, ganz wie in der Physik, und die so erschaffenen Dinge in Prozessen begreifbar, greifbar und handhabbar macht.
Unsere Existenz durch eine stabile und sich entwickelnde Psychosomatik
Wir sind in einen Dialog zwischen unserem Bewusstsein und unserem Unterbewusstsein verwickelt
Unsere Überlegungen haben durchaus eine tiefe Verbindung zu unserem Leben. Auch, wenn es einem als Mensch der heutigen „modernen“ Zeit erstaunlich erscheinen kann, dass wir aus dieser bedeutenden mathematisch-naturphilosophischen Sicht an die Wurzeln des Lebens gelangen.
Denn aus meinem Verständnis heraus basiert unser Leben, unsere Psyche und Psychosomatik, auch auf unserem inneren Dialog zwischen Bewusstsein und Unterbewusstsein. Dieser Dialog ist unter anderem durch unseren Fokus bestimmt und dadurch ob gerade unser Bewusstsein, im Wachzustand, oder unser Unterbewusstsein, im Schlaf, im Vordergrund ist.
Durch die vorangegangenen Überlegungen lernen wir mehr darüber, wie unser Fokus funktioniert und welche Aspekte und Ebenen er hat. Und darüber, wie unser Fokus mit Antimengen und negativen Zahlen verbunden ist, lernen wir unser Bewusstsein und Unterbewusstsein besser zu verstehen.
→
| |
Neue Einsichten |
|
Die ontologische Struktur beinhaltet die Zählrichtung
←
Wir können durch das Vorstehende erkennen, dass aus ontologischer Sicht die Null – die leere Menge –, aufgrund des Ausgangs vom Zählen, zu den positiven Zahlen gehört, und dadurch die natürlichen Zahlen \( \mathbb{N} \), einschließlich der Null, bildet.
Eine fundamentale Asymmetrie
Die ontologische Struktur der Zahlen beinhaltet die Zählrichtung
| ▾ | Notizen |
Eine Asymmetrie zwischen Existenz und ihrer Assoziation
• Hier wird ebenso eine Asymmetrie zwischen einer ontologischen Existenz und ihrem assoziierten „Wert“ aufgezeigt.
| ▾ | Zwischenzeitlicher, wohl falscher Text: |
Interessanterweise können wir so erkennen, dass aus ontologischer Sicht die Null – die leere Menge –, aufgrund des Ausgangs vom Zählen, zu den positiven Zahlen gehört, und dadurch die natürlichen Zahlen \( \mathbb{N} \), einschließlich der Null, bildet.
Da es zur Null keine Antimenge und damit auch ontologisch kein negatives Komplementär gibt, was perfekt zur Eindeutigkeit und gewünschten Bidirektionalität in Bezug auf die Zahlenwerte passt, gibt es tatsächlich genauso viele negative wie positive Zahlen, eben beides ohne die Null.
Es gibt also eine fundamentale Asymmetrie zwischen der ontologischen Struktur der Ordinalzahlen und der ontologischen Struktur der aus ihnen abgeleiteten negativen Zahlen. Dies gilt also auch für alle endlichen ganzen positiven Zahlen mit der Null und für die endlichen ganzen negativen Zahlen, ohne die Null:
Sei \( \# \) das Symbol für den Operator, der die Anzahl der Elemente einer Menge liefert,
so gilt, auch wegen der oben definierten Gleichsetzung von Anzahlen und deren entsprechenden Mengen:
Die Summe aller endlichen ganzen Zahlen ist demnach Null:
Der Durchschnitt aller endlichen ganzen Zahlen ist demnach Null:
(In Arbeit …)
Interessanterweise ergibt sich so, dass es eine negative Zahl mehr gibt als positive Zahlen, ohne die Null. Wie kann das sein?
Ontologische Begründung
Aus ontologischer Sicht, also aus Sicht der Struktur des Seins oder die Realität betreffend, hat mir mein Freund Raimund Welsch nahegelegt:
Begreifen wir jede nach oben gezählten Abstand Eins als Welle – oder alternativ als Sägezahn, wie ich es selber schon früher gedacht hab – dann fängt jede dieser Wellen bei einer ganzen
Zahl an.
Die darauf folgende nächste ganze Zahl ist schon der Beginn der nächsten Welle und gehört nicht mehr zu der, die wir gerade gezählt haben.
Die nullte Welle oder der nullte Zahn beginnt also bei der Null und endet vor der Eins.
|
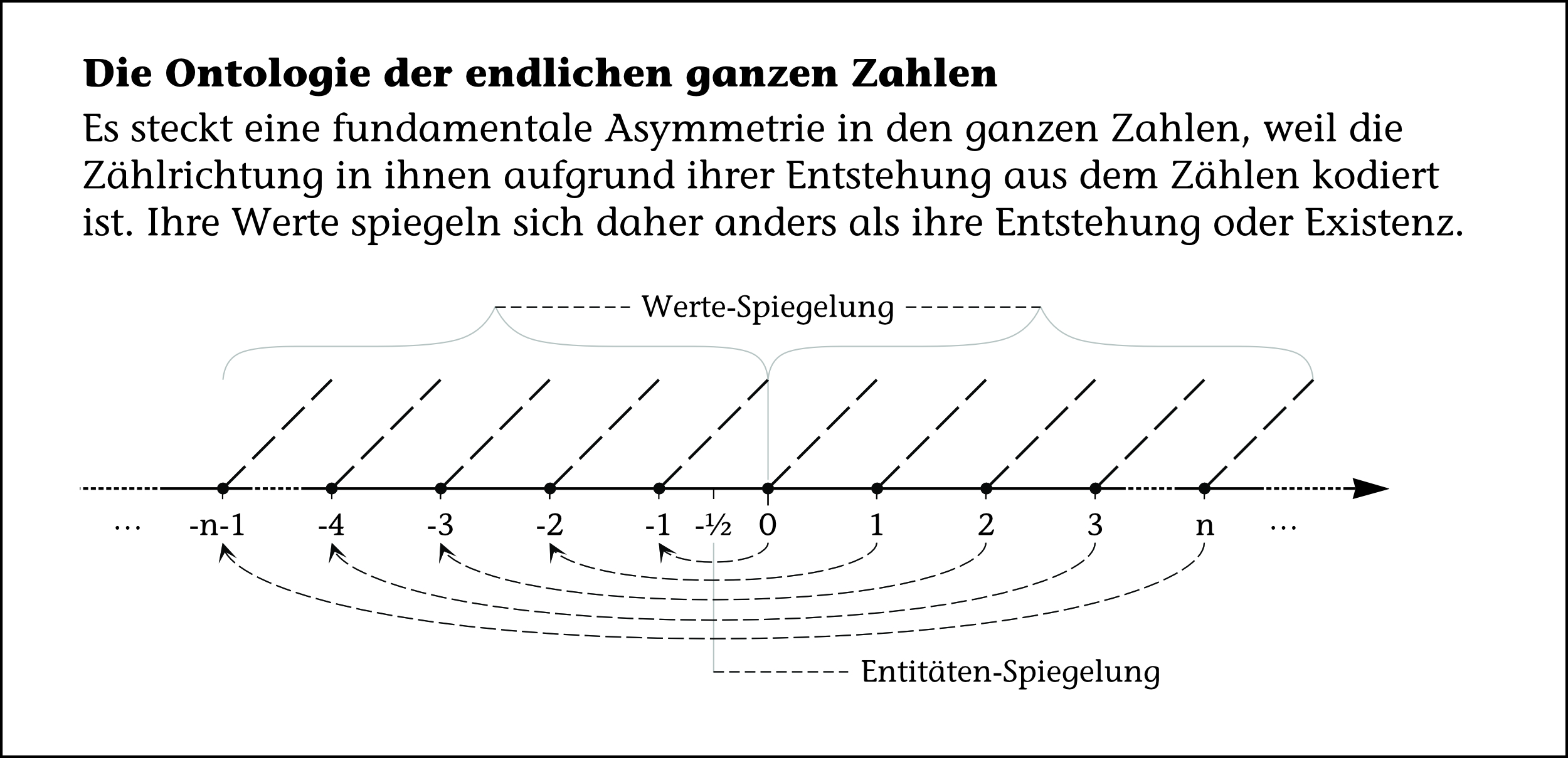
Würden wir die natürlichen Zahlen einfach an der Null spiegeln, um die negativen ganzen Zahlen zu erhalten, dann hätten wir die Null doppelt in der Struktur; eine gehörte zu den positiven und eine zu den negativen Zahlen, was nicht eindeutig wäre. Auch würde sich in den negativen ganzen Zahlen die Zählrichtung umkehren und dadurch könnten wir die negativen Zahlen nicht mehr in ihrer Struktur von den positiven Zahlen unterscheiden. Denn das scheinbare Rückwärtszählen wäre ja doch in Wirklichkeit so auch ein Vorwärtszählen. Beide Zahlentypen wären identisch, was ontologisch keinen Sinn ergibt.
Sinn erhalten wir, wenn wir erkennen, dass die negativen ganzen Zahlen aus den verschobenen natürlichen Zahlen entstehen, unter Erhalt der Zählrichtung, durch Welle oder Zahn verdeutlicht (siehe ). Während also der auf die negative Seite verschobene Nullpunkt eine negative Zahl repräsentiert, nämlich die minus Eins, repräsentiert der originale Nullpunkt keine positive Zahl, sondern die Null selber. Die Vollständigkeit der negativen und damit aller ganzen Zahlen entsteht dadurch, dass wir durch vollständige Induktion alle natürlichen Zahlen ins negative verschieben.
Ontologisch betrachtet sind negative Zahlen also nicht die inklusive der Zählrichtung an der Null gespiegelten natürlichen oder alternativ nur positiven Zahlen. Sondern es handelt sich strukturell um eine Verschiebung, die die Zählrichtung beibehält und nicht spiegelt, wohingegen die repräsentierten Werte an der Null gespiegelt sind.
Wir erkennen: Auch, wenn wir nur auf die , schwingt das ontologisch implizite Vorhandensein, die Existenz, der Zwischenräume zwischen den ganzen Zahlen und wie diese mit ihnen verbunden sind, mit. Denn die Intervalle der Zwischenräume, die an den ganzen Zahlen in Zählrichtung hängen, sind der Grund für die Zahlenwert-Symmetrie, die sich an der Null spiegelt.
Kombinatorische Begründung
Schauen wir uns hier noch einmal die oben stehenden Formeln und an:
Wir können am Übergang von zu sehen, dass wir so viele endliche Zahlen am Mengenuniversum weglassen können, wie es von ihnen gibt: derer in der Anzahl \( ω \) existieren, nämlich ein Mal die vollständige Induktion der natürlichen Zahlen. Jede dieser zusätzlich weggelassenen endlichen Zahlen steht für jeweils eine negative ganze Zahl.
Demnach gibt es also genau so viele negative ganze Zahlen, wie positive ganze Zahlen mit der Null existieren. Und diese kombinatorische Anzahl wird in \( -ω \) ausgedrückt und ihr absoluter Wert ist eben \( ω \). Also gibt es auch aus dieser Perspektive eine negative ganze Zahl mehr, als es positive ohne die Null gibt.
Formulierung der Entstehung der negativen ganzen Zahlen durch Rückwärtszählen, ohne Umkehrung der Zählrichtung
Um auszudrücken, wie jede negative ganze Zahl jeweils aus einer natürlichen Zahl entsteht, berücksichtigen wir
im Ansatz die oben entwickelte, ontologische Vorstellung, dass es sich bei Zahlen quasi um Wellen – oder Sägezähne – von einer Zahl zur nächsten handelt.
Diese Wellen hängen in Zählrichtung an den Zahlen.
Die negativen Zahlen entstehen also nicht durch eine Spiegelung dieser Wellen, sondern durch deren Verschiebung. Und dies soll sich in der ersten Struktur der Formulierung ausdrücken:
Die Intervalle, die zwischen den Zahlen liegen, hängen an der vorstehenden ganzen Zahl und werden auf diese Weise mit verschoben, was wir bei den Superial-Zahl noch expliziter erkennen können. Daher steht quasi am „Beginn“ der endlichen negativen ganzen Zahlen auch der Punkt einer ganzen Zahl, was eben der Grund dafür ist, dass es eine endliche negative ganze Zahl mehr geben muss, als positive, ohne die Null. Denn das Zählen ist die Grundlage aller Zahlen.
Wenn wir die Verschiebung vereinfachend umformen:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\mathbb{Z}^{-}\;\;\;=\;\;\;\left\{\; x\;~\middle|~\;\left( \forall n \in \mathbb{N} \right) \left[\; x = n - 2 \cdot n - 1 \;\right] \;\right\} } \] | (BO.Ein.NE.2) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\mathbb{Z}^{-}\;\;\;=\;\;\;\left\{\; x\;~\middle|~\;\left( \forall n \in \mathbb{N} \right) \left[\; x = - n - 1 \;\right] \;\right\} } \] | (BO.Ein.NE.3) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\mathbb{Z}^{-}\;\;\;=\;\;\;\left\{\; x\;~\middle|~\;\left( \forall n \in \mathbb{N} \right) \left[\; x = - \left( n + 1 \right) \;\right] \;\right\} } \] | (BO.Ein.NE.4) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\# \mathbb{Z}^{-}\;\;\;=\;\;\;ω } \] | (BO.Ein.NE.5) | ||
Dann entsteht der Eindruck einer Spiegelung.
Anzahl der endlichen ganzen Zahlen
So kommen wir zu Aussagen über die Anzahl der ganzen endlichen Zahlen:
Sei \( \# \) das Symbol für den Operator, der die Anzahl der Elemente einer Menge liefert,
so gilt, auch wegen der oben definierten Gleichsetzung von Anzahlen und deren entsprechenden Mengen
was damit gezeigt werden sollte.
Diese Aussagen sind durchaus bemerkenswert und führen uns zu einer fundamentalen und sehr spannenden Asymmetrie.
Daraus folgt eine prinzipielle Asymmetrie
Auf diese Weise ergibt sich innerhalb der endlichen, ganzen Zahlen eine prinzipielle und fundamentale Asymmetrie,
die sich in der Summe über alle endlichen, ganzen Zahlen zeigt,
weil jede negative ganze Zahl um minus Eins kleiner ist, als die natürlich Zahl, aus deren Verschiebung sie gebildet wird (siehe ):
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ \forall z \in \mathbb{Z}} z\;\;\;=\;\;\;\sum_{ \forall n \in \mathbb{N}} n - \sum_{ \forall n \in \mathbb{N}} \left( n + 1 \right) } \] | (BO.Ein.NE.9) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sum_{ \forall z \in \mathbb{Z}} z\;\;\;=\;\;\;\sum_{ \forall n \in \mathbb{N}} n - \sum_{ \forall n \in \mathbb{N}} n - \sum_{ \forall n \in \mathbb{N}} 1 } \] | (BO.Ein.NE.10) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sum_{ \forall z \in \mathbb{Z}} z\;\;\;=\;\;\;- \sum_{ \forall n \in \mathbb{N}} 1 } \] | (BO.Ein.NE.11) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\sum_{ \forall z \in \mathbb{Z}} z\;\;\;=\;\;\;- ω } \] | (BO.Ein.NE.12) | ||
In Worten ausgedrückt bedeutet dies:
Die Summe aller endlichen, ganzen Zahlen ist demnach der aktual unendliche Wert \( –ω \) und nicht \( 0 \) (Null), wie wir im Allgemeinen eher annehmen.
Der Wert \( –ω \) dieser Summe ist nur mit Biordinalzahlen ausdrückbar.
Das die Summe aller endlichen ganzen Zahlen negativ ist, dürfte den einen oder anderen erstaunen. Denn naiv neigen wir wohl zumeist dazu anzunehmen, dass sich alle endlichen ganzen Zahlen zu Null summieren, weil wir von einer Werte- und Zahlensymmetrie bei Null ausgehen. Das wirklich \( –ω \) die Summe aller endlichen ganzen Zahlen ist und ebenso auch \( 2 ω \) die Anzahl aller endlichen ganzen Zahlen, bestätigt sich durch die plausible Herleitung der Integration auf Basis der Superial-Zahlen, wenn wir die dabei auftretenden aktual unendlichen Summen genauer untersuchen.
Der Mittelwert aller endlichen, ganzen Zahlen ergibt sich dann, wenn wir, wie üblich, die Summe durch die Anzahl ihrer Summanden teilen, zu:
In Worten ausgedrückt bedeutet dies:
Der Mittelwert aller endlichen, ganzen Zahlen ist demnach \( –½ \) und nicht \( 0 \) (Null), wie wir im Allgemeinen eher annehmen.
Das ist möglicherweise für den einen oder anderen eine überraschende Erkenntnis. Ich finde sie hochspannend.
| ▾ | Möglicher Bezug zur analytischen Fortsetzung der Riemannschen Zeta-Funktion: |
Notiz
| • |
Bezüge zur Riemannschen Zeta-Funktion |
Die oben erzielte Erkenntnis, dass der Mittelwert aller endlichen, ganzen Zahlen \( -½ \) und damit ein endlicher, negativer Wert ist, erinnert stark an ein in gewisser Hinsicht erstaunliches Ergebnis in Bezug auf die Riemannsche Zeta-Funktion \( \zeta(s) \) beim Funktionswert \( 0 \):
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \zeta(0)\;\;\;=\;\;\;- \frac{ 1 }{ 2 } } \] | (BO.Ein.NE.16) |
Wo der (mögliche) Zusammenhang besteht, werden wir gleich noch weiter ausführen.
Ein in der Mathematik ganz berühmtes Ergebnis, dass unter anderem durch den indischen Mathematiker Srinivasa Ramanujan(Verweis) gefunden wurde, liegt beim Funktionswert \( -1 \) der Zeta-Funktion:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \zeta(-1)\;\;\;=\;\;\;- \frac{ 1 }{ 12 } } \] | (BO.Ein.NE.17) |
(In Arbeit …) Versuch nach Definition der Zeta-Funktion durch die Dirichletsche Eta-Funktion
Allerdings gilt die simple Definition der Zeta-Funktion nur für komplexe Funktionswerte, dessen Realteil größer als \( 1 \) ist:
Dass die Summe unendlich vieler Einsen oder die Summe aller natürlichen Zahlen einen endlichen, negativen Wert ergeben soll, erscheint hier sehr merkwürdig. Allerdings ist in dieser Definition der Zeta-Funktion der Funktionswert \( -1 \) ja eben auch nicht definiert.
Berücksichtigen wir, dass die Zeta-Funktion mit Hilfe der Dirichletschen Eta-Funktion(Verweis) \( \eta(s) \) ihre sogenannte analytische Fortsetzung findet, dann erhalten wir für die Definition von \( \zeta(s) \):
Dies gilt unter der Voraussetzung, dass wir eine Definition von \( \eta(s) \) über die ganze komplexe Zahlenebene \( \mathbb{C} \) finden.
Wir beginnen einmal mit der einfachsten Definition der Dirichletschen Eta-Funktion:
Hier erkennen wir schon eine gewisse Ähnlichkeit mit unserer Formel , auch, wenn diese Definition eigentlich nicht für die Funktionswerte \( 0 \) und \( -1 \) gilt.
Addieren wir doch trotzdem mal die positiven und negativen Einsen und schauen, wann wir vielleicht \( ½ \) erhalten. Aus dem Mathologer Video Numberphile v. Math: the truth about 1+2+3+...=-1/12 wissen wir, dass die Summe über die Ramanujan Summation als eine Art Mittelwert definiert ist. Benutzen wir die Formel von oben, dann ergibt sich:
Hier erkennen wir, dass das Ergebnis ganz entscheidend von der Anzahl der Elemente in \( \mathbb{N} \setminus \left\{ 0 \right\} \) abhängt. Ist die Anzahl gerade, dann erhalten wir \( 0 \).
(In Arbeit …)
Addieren wir doch auch mal die positiven und negativen Zahlen und schauen, wann wir vielleicht \( ¼ \) erhalten:
Für die Summe aller natürlicher Zahlen können wir die Gaußsche Summenformel benutzen:
(In Arbeit …)
(In Arbeit …) Versuch nach Definition der Zeta-Funktion durch die Dirichlet-Reihe
Nach der Definition der Zeta-Funktion durch die Dirichlet-Reihe könnten wir naiver Weise annehmen, die Summe aller endlichen, natürlichen Zahlen hätte ein negatives Ergebnis:
Allerdings gilt diese Definition der Zeta-Funktion nur für komplexe Funktionswerte, dessen Realteil größer als \( 1 \) ist.
Dennoch betrachten wir einmal, was das Ergebnis wäre:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \sum_{ n = 1 }^{\infty} n\;\;\;=\;\;\;1 + 2 + 3 + 4 + \cdots\;\;\;\overset{?}{=}\;\;\;- \frac{ 1 }{ 12 } } \] | (BO.Ein.NE.56) |
(In Arbeit …) Siehe Gaußsche Summenformel
(In Arbeit …) Versuch nach Primzahlprodukt-Vermutung
Nach der Primzahlprodukt-Vermutung ist \( ω \) eine aktual unendliche, gerade Zahl und das Ergebnis damit eine aktual unendliche, ganze Zahl. Insofern passt dies. Es ist noch nicht geklärt, wie dies durch Mengen im hier entwickelten Sinn dargestellt werden kann.
(In Arbeit …)
Was wäre wenn:
(In Arbeit …)
Die Summe aller endlichen, natürlichen Zahlen, ohne die Null, hätte tatsächlich ein negatives Ergebnis. Das ist aber eigentlich unmöglich.
Es stellen sich allerdings mehrere Fragen: Zum einen, was wäre nach der Ausgangsformel, wenn wir die Null doch berücksichtigen?
(In Arbeit …)
Neue Einsichten zu positiven aktual unendlichen Biordinalzahlen
Wir können nun zu Aussagen kommen, die etwas über die Größe von \( ω \) verraten:
Subtrahieren wir eine beliebige endliche natürliche Zahl \( n \) von \( ω \), ergibt sich niemals eine Zahl, die zur Menge der endlichen Zahlen gehört:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall n \in \mathbb{N} \right) \left[\; ω - n\;\;\;\notin\;\;\;\mathbb{N} \;\right] } \] | (BO.Ein.NE.65) |
\( ω – n \) ist nicht in den natürlichen Zahlen \( \mathbb{N} \), weil eine unendlich große Zahl \( ω \) minus einer endlichen Zahl \( n \) eine unendlich große Zahl bleibt. Dies ist offensichtlich und plausibel. Und eine unendlich große Zahl ist eben per Definition kein Element von \( \mathbb{N} \).
In den Biordinalzahlen zeigt sich also eine riesige mit unendlich großen ganzen Zahlen gefüllte Lücke zwischen den endlichen natürlichen Zahlen und \( ω \).
Hier sei gesagt, dass diese Lücke auch ein wesentlicher Grund dafür ist, dass die Primzahlprodukt-Vermutung wahr sein könnte. (Ist das wirklich eine Begründung? Die Lücke ist so groß nun auch wieder nicht, siehe unten. Außerdem geht es ja um den Wert von \( ω \), der sich aus dem Produkt aller endlichen Primzahlen ergeben soll, und nicht darum, wieviele ganze Zahlen vor \( ω \) kommen.)
Diese Lücke hat eine wichtige Bedeutung.
Es gibt mehr ganze Zahlen von Null bis zu \( ω \), als der Wert von \( ω \) ausdrückt
Eine Paradox erscheinende, bizarre Situation
Doch was ist geschehen? Und was bedeutet das?
Gehen wir noch einmal zurück zur Definition der Ordinalzahlen:
Die Ordinalzahlen sind so definiert, dass nach den endlichen natürlichen Zahlen gleich \( ω \) folgt:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left\{ 0, 1, 2, 3, 4, 5, \cdots , ω \right\} } \] | (BO.Ein.NE.66) |
Allerdings existiert ein Bereich, der nur analytisch durchleuchtet werden kann, weil er für die vollständige Induktion des Zählens steht. Dieser Bereich wird durch die Ellipse (Dreipunkte-Symbol) „\( \cdots \)“ ausgedrückt.
Nach der Definition der Ordinalzahlen kommen vor \( ω \) also genau so viele ganze Zahlen, wie die Anzahl \( ω \). Denn das ist explizit so definiert.
Erweitern wir die Ordinalzahlen nun in Form der Biordinalzahlen zu einem Ring und führen damit die Subtraktion endlicher natürlicher Zahlen von \( ω \) ein, dann entstehen zwangsweise weiter ganze Zahlen zwischen der Ellipse und \( ω \):
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left\{ 0, 1, 2, 3, \cdots , \cdots , ω - 3, ω - 2, ω - 1, ω \right\} } \] | (BO.Ein.NE.67) |
Eine ganz wesentliche und nicht ganz so einfach zu beantwortende Frage ist: Wieviele Zahlen sind nun vor \( ω \) zusätzlich neu entstanden?
Die Antwort darauf haben wir im Abschnitt ausführlich beleuchtet und eine plausible Antwort aus ontologischer und aus kombinatorischer Perspektive gefunden. Es kommen \( ω \) weitere Zahlen hinzu:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\# \left\{ 0, 1, 2, \cdots , \cdots , ω - 2, ω - 1 \right\}\;\;\;=\;\;\;2 \cdot ω } \] | (BO.Ein.NE.68) |
Wie wir erkennen können, liegen nun vor \( ω \), mit der Null, dann \( 2 ω \) ganze endlich und unendlich große Zahlen. Das erscheint ein wenig paradox.
Trotzdem ist die Erweiterung ontologisch erkenntnisreich, plausibel und sinnvoll, weil nützlich. Denn, wie wir noch sehen werden, können wir so überhaupt erst die Anzahl der Zahlen in bestimmten Mengen ausdrücken.
Eine größere Anzahl von Vorgängern, als eine Zahl groß ist, kennen wir schon von rationalen Zahlen
Bei den Biordinalzahlen haben wir es offenbar mit einer Mischform auf dem Weg zu den rationalen Zahlen zu tun.
Denn auch bei den rationalen Zahlen haben wir mehr Vorgänger, sagen wir beispielsweise vor der \( ½ \), als die Zahl groß ist. Mit der und nach der Null und vor der \( ½ \) liegen sogar unendlich viele rationale Zahlen. Nur handelt es sich nicht um ganze Zahlen, sondern die rationalen Zahlen liegen dicht(Verweis), während die Biordinalzahlen alle noch ganze Zahlen sind und noch nicht dicht liegen.
Bezug zu den Superial-Zahlen und zur Anzahl der rationalen Zahlen
Das vorstehende Ergebnis spielt bei der Analyse der Struktur der Superial-Zahlen und damit auch im Hinblick auf
die Anzahl der rationalen Zahlen eine zentrale Rolle.
Bemerkenswerter Weise hat die superiale Basis \( \s \) dann wieder genau so viele natürliche Vorgänger, wie sie selber groß ist.
Die Summe aller natürlichen Zahlen
So kommen wir mit den neuen Zahlen beispielsweise auch in die Lage, die Summe aller natürlichen Zahlen zu berechnen.
Für die Summe aller natürlicher Zahlen können wir die Gaußsche Summenformel benutzen, wen wir sie entsprechend anpassen:
Wandeln wir die Gaußsche Summenformel mit Hilfe der obigen Mengendefinitionen von Zahlen
nun so ab, dass wir uns nicht auf das größte Element der Summe beziehen,
sondern auf die Anzahl an Elementen, die davor zu summieren sind, dann müssen wir
den letzten Summanden abziehen:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \left( \forall n \in \mathbb{N} \right) \left[\; \sum_{ ( \forall i \in \mathbb{N} )[i \leqslant n] } \!\!\!\! i\;\;\;=\;\;\;0 + 1 + 2 + 3 + \cdots + n \;\right] } \] | (BO.Ein.NE.69) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\left( \forall n \in \mathbb{N} \right) \left[\; \sum_{ ( \forall i \in \mathbb{N} )[i \leqslant n] } \! i\;\;\;=\;\;\;\frac{ n^{2} + n }{ 2 } \;\right] } \] | (BO.Ein.NE.70) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\left( \forall n \in \mathbb{N} \right) \left[\; \sum_{ \forall i \in n + 1 } \! i\;\;\;=\;\;\;\frac{ n^{2} + n }{ 2 } \;\right] } \] | (BO.Ein.NE.71) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\left( \forall n \in \mathbb{N} \right) \left[\; \sum_{ \forall i \in n } i\;\;\;=\;\;\;\frac{ n^{2} + n }{ 2 } - n \;\right] } \] | (BO.Ein.NE.72) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\left( \forall n \in \mathbb{N} \right) \left[\; \sum_{ \forall i \in n } i\;\;\;=\;\;\;\frac{ n^{2} + n - 2 n }{ 2 } \;\right] } \] | (BO.Ein.NE.73) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\left( \forall n \in \mathbb{N} \right) \left[\; \sum_{ \forall i \in n } i\;\;\;=\;\;\;\frac{ n^{2} - n }{ 2 } \;\right] } \] | (BO.Ein.NE.74) | ||
Um daraus eine allgemeine Formel für aktual unendlich große Mengen zu definieren, scheint es mir sinnvoll uns auf Mengen zu beschränken, die ausschließlich von der Null an ganze Zahlen enthalten. Wir definieren also die Menge \( \mathbb{N}_{\infty} \) aller positiven ganzen Zahlen, von der Null an bis ins beliebig aktual Unendliche. Diese Menge können wir mit Hilfe der Abrundung durch die Gaußklammer \( \lfloor x \rfloor \) zum Ausdruck bringen, die eine Zahl \( x \) auf die nächst kleinere ganze Zahl abrundet, wenn sie noch keine ganze Zahl ist:
Die Elemente sowohl der Ordinalzahlen sowie die der Biordinalzahlen gehören offensichtlich auch zu \( \mathbb{N}_{\infty} \):
Desweiteren soll es sich um Mengen \( \mathbb{N}_{\infty,c} \) ganzer Zahlen handeln, in denen der Wert jedes Elements die Anzahl an Elementen in der Menge wiedergibt, die vor ihm kommen. Diese Mengen fassen wir in der Klasse \( \mathbb{K}_{\infty,c} \) der Anzahl äquivalenten Mengen zusammen:
Die Definition der Ordinalzahlen erfüllt dieses Kriterium offensichtlich, während die Biordinalzahlen es nicht erfüllen
weil die Biordinalzahlen eben .
Und von hier kommen wir zur Klasse Gauß-Summen äquivalenter Mengen. Dies sind unendlich große Mengen, in denen für jedes Element die oben angepasste Gaußsche Summenformel gilt
Und am Rande vermute ich, dass eine Menge, die in der Klasse der Gauß-Summen äquivalenten Mengen ist auch zur Klasse der Anzahl äquivalenten Mengen gehören muss
was zu beweisen ist.
So können wir nun zur Summe aller endlichen natürlichen Zahlen übergehen
die wir ja errechnen wollten.
Interessanterweise lässt sich diese Summe nur mit den Biordinalzahlen ausdrücken, wie wir an der Differenz sehen. Die in dieser Arbeit entwickelten Zahlen sind also auch im Zusammenhang mit Ordinalzahlen von Bedeutung.
Und die Summe setzt voraus, dass \( ω^{2} – ω \) gerade ist, also ganzzahlig durch Zwei geteilt werden kann. Das bedeutet, dass die Zwei als Faktor in beiden Summanden stecken muss. Folglich trägt \( ω \) den Primfaktor \( 2 \) in sich. Dies ist eine weitere Bestätigung der Plausibilität des Beweises der Primzahlprodukt-Vermutung.
Interessant wäre, ob sich durch die Bestimmung weiterer Summen die Plausibilität des Beweises der Primzahlprodukt-Vermutung vertiefen lässt. Siehe Mathologer: The Moessner Miracle. Why wasn't this discovered for over 2000 years?
Die Menge der Ordinalzahlen nur ins Negative erweitert
Die Limeszahlen in negativer Zählrichtung erhalten, ohne Vorgänger, und so positive wie negativen Zahlen adressieren
Wollen wir alle natürlichen Zahlen \( n \) adressieren, von der Null an bis ins potenziell Unendliche, dann nutzen wir dafür die Menge der natürlichen Zahlen \( \mathbb{N} \) durch \( n \in \mathbb{N} \) oder mit dem Symbol \( ω \) der Ordinalzahlen oder Biordinalzahlen durch \( n \in ω \). Wenn wir mehr Zahlen, auch im aktual Unendlichen, dazu nehmen wollen, dann geht dies zum Beispiel durch \( n \in 2 ω \).
Die Elemente einer Teilmenge erreichen wir dann durch \( n \in [5, 897]_{\mathbb{N}} \) oder \( n \in [5, 897]_{ω} \) oder \( n \in [5, 897]_{\mathbb{On}} \), deren Teilmengen alle gleich sind, auch, wenn sich die Basismengen teilweise unterscheiden.
Oder im anderen Fall über \( n \in [5, ω + 56]_{2 ω} \) oder \( n \in [5, ω + 56]_{\mathbb{On}} \), deren Teilmengen ebenfalls alle gleich sind, auch, wenn sich die Basismengen unterscheiden.
Anders bei ganzen Zahlen
Es gibt Fälle, in denen wir Mengen aller endlichen ganzen Zahlen, aber dazu auch von ihrem Wert her über das endliche hinausgehende
aktual unendliche ganze Zahlen benötigen.
Und zwar auch im negativen Bereich.
Ein solcher Fall tritt auf, wenn wir die arithmetische Struktur der Geometrie untersuchen.
Denn wir wollen dort alle Punkte in einem Netz unendlich vieler Teilungen adressieren, das sich auch über die
ganzen negativen Zahlen erstrecken soll.
In diesem Fall kommen wir aber mit den Biordinalzahlen \( \mathbb{Bn} \) nicht weiter, weil sie für alle Limeszahlen Vorgänger
und Nachfolger haben und das sind zu viele Adressen.
Sondern wir brauchen die Ordinalzahlen einfach noch einmal in negativer Richtung gespiegelt.
Wollen wir alle endlichen ganzen Zahlen \( z \) adressieren, positive wie negative, dann können wir dies über die Menge der ganzen Zahlen \( \mathbb{Z} \) mit \( z \in \mathbb{Z} \) tun. Eine Teilmenge erhalten wir über \( z \in [-5, 897]_{\mathbb{Z}} \). Kein Problem.
Jedoch schon im Falle der Teilmenge \( z \in [-5, ω + 56]_{\mathbb{Bn}} \) würden wir Zahlen wie \( [ -5, -4, -3, -2, -1, 0, 1, 2 \cdots ω - 3, ω - 2, ω - 1, ω, ω + 1, ω + 2 \cdots ] \) erhalten. Davon sind Zahlen mit Differenzen, wie \( ω - 1 \), aber eben keine Zahlen, die wir in diesem Fall adressieren wollen.
Ebenso nicht im Falle der Teilmenge \( z \in [- (ω + 87), ω + 56]_{\mathbb{Bn}} \) mit Zahlen wie
wo auch \( - (ω - 1) \) oder \( - (ω - 2) \) nicht dazu gehören sollten.
Die Biordinalzahlen sind also als Basismenge der Intervall-Menge nicht geeignet. Wir benötigen eine Basismenge, die die Ordinalzahlen enthält und zusätzlich auch gleiche, die entsprechend der , ins Negative gespiegelt und verschoben sind, enthält:
So erhalten wir die Basismenge, die wir zum Adressieren benötigen.
Weiterentwicklung zu den Superial-Zahlen
Die superiale Basis \( \s \) hat \( \s \) natürliche Superial-Zahlen als Vorgänger
Die Superial-Zahlen können in gewisser Hinsicht als Weiterentwicklung der Biordinalzahlen zu einer abelschen Gruppe bezüglich der Addition und Multiplikation verstanden werden und sie sind sogar ein angeordneter algebraischer Körper. Dies gilt in einem noch engeren Sinn, wenn sich die Primzahlprodukt-Vermutung als wahr herausstellen sollte.
Auch, wenn mir noch keine explizite Mengendarstellung der Superial-Zahlen bekannt ist, die der der Biordinalzahlen entspricht, so waren für mich die Superial-Zahlen und ihre Eigenschaft, dass die Subtraktion vollständig definiert ist, der Anlass zur Entwicklung der Biordinalzahlen aus den Ordinalzahlen, um die ontologische Struktur von aktual unendlichen Zahlen besser zu verstehen. Daher liegt es auf der Hand, deren Eigenschaften in Bezug auf ihre Vorgänger zu vergleichen.
Mit den Ordinalzahlen und den Biordinalzahlen befinden wir uns strukturell sozusagen am Sockel der Fraktalität des Aktual-Unendlichen. Dies erscheint mir ein Grund dafür, dass wir in bizarre und auch interessante, scheinbar paradoxe Situationen kommen.
Mit den Superial-Zahlen kommen wir dann quasi in die höheren Sphären der Fraktalität, was zur Folge hat, dass uns die Dinge wieder harmonischer erscheinen. Denn in den natürlichen Superial-Zahlen haben wir wieder so viele Vorgänger, wie der Wert einer bestimmten natürlichen Superial-Zahl groß ist.
| |
Fußnoten |
|
| 1. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl. | |
| 2. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ring (Algebra). | |
| 3. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Riemannsche Vermutung. | |
| 4. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl, Die natürlichen Zahlen als geordnete Mengen. | |
| 5. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Peano-Axiome, Axiome, Ursprüngliche Formalisierung. | |
| 6. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Geordneter Körper, Definition. | |
| 7. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Unendlichkeitsaxiom, Formulierung; Bedeutung für die Mathematik, Natürliche Zahlen. | |
| 8. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Allklasse. | |
| 9. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Ordinalzahl, Motivation und Definition, Limes- und Nachfolgerzahlen. | |
| 10. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Unendlichkeitsaxiom, Formulierung; Bedeutung für die Mathematik, Natürliche Zahlen. | |
| 11. | Vgl. Wikipedia, Riemannsche Zeta-Funktion. | |
| 12. | Vgl. Wikipedia, Riemannsche Zeta-Funktion, Geschichte, Anfang des 20. Jahrhunderts, Ramanujans Arbeit zur Zeta-Funktion. | |
| 13. | Vgl. Wikipedia, Riemannsche Zeta-Funktion, Definition und Darstellungsformen, Methoden zur analytischen Fortsetzung, Umformungen der Dirichlet-Reihe und die Eulersche Reihentransformation. | |
| 14. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Gaußsche Summenformel. | |
| 15. | Vgl. Wikipedia, Riemannsche Zeta-Funktion, Definition und Darstellungsformen, Dirichlet-Reihe. | |
| 16. | Vgl. Wikipedia, Riemannsche Zeta-Funktion, Geschichte, Anfang des 20. Jahrhunderts, Ramanujans Arbeit zur Zeta-Funktion. | |
| 17. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Gaußsche Summenformel. | |
| 18. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Gaußsche Summenformel. | |
| 19. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Abrundungsfunktion und Aufrundungsfunktion. | |
| 20. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Abelsche Gruppe. | |
| 21. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Körper (Algebra). |
| |
Stand 05. September 2024, 14:00 CET.
-
Permanente Links:
(Klicke auf die Archivlogos
zum Abruf und Ansehen
der Archive dieser Seite.) -
-
archive.todaywebpage capture
