Elektroschwache Wechselwirkung, Teilchenumwandlungen und innerer Spin
Das neue Teilchenmodell gibt der elektroschwachen Kraft und ihrem schwachen Isospin eine reale Ursache.
Der neue, innere Spin, als eine der realen Ursachen des schwachen Isospins, ergibt sich aus der Vereinheitlichung von Quantenmechanik und Allgemeiner Relativitätstheorie.
| ▾ | Notizen |
Virtuelle Photonen
• Im Falle der Wirkungsquanten (Transversalwellen) sind ihre abgestrahlten virtuellen Wirkungsquanten Longitudinalwellen (siehe Vereinfachtes Modell der Quantengravitation, Abbildung 2). Photonen sind ja auch Transversalwellen und, so denke ich, analog dazu sind auch ihre abgestrahlten, rein elektromagnetischen virtuellen Photonen Longitudinalwellen.
• Im Leptonen-Modell haben wir es hingegen mit einer Mischung zu tun:
⋅ In ihm (siehe ) wird deutlich, dass seine einem Photon ähnlichen Strukturen eine Mischung aus Transversal- und Longitudinalwelle sind, die dazu auch noch in ihrer Größe pulsiert. So müssen auch ihre abgestrahlten virtuellen Photonen eine Mischung aus pulsierender Transversal- und Longitudinalwelle sein.
⋅ Diese Mischung sollte etwas mit dem Weinberg-Winkel zutun haben.
⋅ Interessant wäre zu untersuchen, wie sich der transversale Anteil der virtuellen Photonen im Verhältnis zu ihrem longitudinalen mit dem Abstand verhält. Also, warum nimmt die schwache Wechselwirkung mit dem Abstand so schnell ab?
Aktuelle fachliche Diskussion
• CP-Verletzung: Es lassen sich keine linkshändigen Antineutrinos nachweisen. Vgl. Uwer, »Teilchen, Antiteilchen und der kleine Unterschied«, S. 15, Kasten.
• Antiteilchen: Symmetriebrechung zwischen Teilchen und Antiteilchen. Warum gibt es mehr Teilchen. Vgl. Uwer, »Teilchen, Antiteilchen und der kleine Unterschied«.
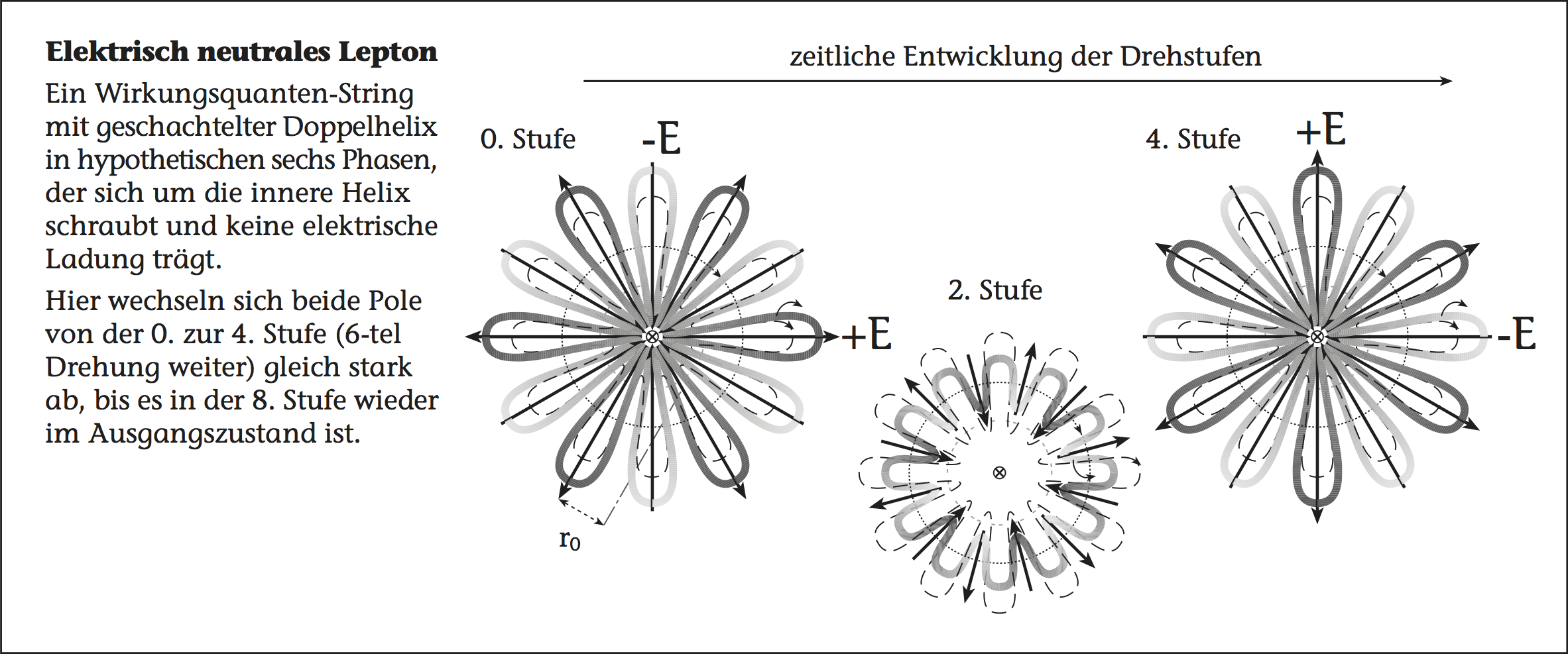
Die eletroschwache Wechselwirkung und der bekannte, schwache Isospin ergeben sich im neuen Elementarteilchenmodell der Quanten-Fluss-Theorie aus der Konfiguration von normalem äußerem Spin, innerem Spin sowie dem Wirkungsquanten-Spin und einer schwingenden des Wirkungsquanten-Strings. Die im nachfolgenden animierte Darstellung eines Leptons stellt den zeitlichen Verlauf einer der möglichen Konfigurationen dar. Genauer wird dies auf der Seite Leptonen-Modell erklärt. Dort wird auch auf den Zusammenhang des inneren Spins mit der Vereinheitlichung von Quantenmechanik und Allgemeiner Relativitätstheorie, unter anderem durch ein neues Verständnis der Zeit, eingegangen.
|
→
Elektromagnetische Wechselwirkung |
|
… entsteht aus einer schwingenden Wirkungsquanten-Polarisation
Hier eher die Wechselwirkung beschreiben. Die Ladung ist im Leptonen-Modell beschrieben …
Die elektrische Ladung des dargestellten Leptons ist ein Mittelwert und entsteht durch die unterschiedlich dichte Verteilung der rot gefärbten Wirkungsquanten auf dem Wirkungsquanten-String:
Ich vermute, dass die dichter und weniger dicht mit Wirkungsquanten bepackten Stellen des Strings eine elektrische Polarisation erzeugen, welche sich in Schwingung befindet. Je weiter diese Stellen unterschiedlicher Dichte auseinander liegen, je größer ist die Polarisation.
Man sieht, dass dieses Lepton während einer Schwingungsphase dann zwischen einem leichter und einem stärker, aber umgekehrt elektrisch polarisierten Zustand schwingt.
Der stärker polarisierte Zustand, wo der Durchmesser oder besser gesagt der innere Radius
des Strings größer ist, dominiert die durchschnittliche Polarisation.
Dieses Lepton ist also insgesamt mit der dichteren Stelle nach außen polarisiert.
Ob dies einem negativ oder einem positiv geladenen Lepton entspricht ist noch ungeklärt.
Bei seinem Antiteilchen wäre die elektrische Polarisation genau umgekehrt.
Das magnetische Drehmoment eines Leptons entsteht durch die Rotation der elektrischen Pole.
Ihre kommt durch deren asymmetrische Verteilung und Dynamik der Pole zustande.
Aufgrund einer etwas anderen Struktur besitzen die im Schnitt keine elektrische Ladung, sehrwohl aber eine schwache Ladung.
→ Elektrische Ladung — Leptonen-Modell
→ Radius — Leptonen-Modell
→ Antiteilchen — Leptonen-Modell
→
| |
Schwache Wechselwirkung |
|
Der schwache Isospin und die kurze Wirkungsdistanz ergeben sich anschaulich aus der Asymmetrie der dynamischen Polarisation
Schaut man sich die Struktur des Leptons in an, so fällt auf, dass die elektrischen Pole während ihrer Bewegung asymmetrisch verteilt sind. Diese asymmetrische und dynamische Polverteilung ist für die schwache Wechselwirkung verantwortlich und hat nur in unmittelbarer Nähe des Leptons oder eine Auswirkung:
Auf größere Distanz gleicht sich die Asymmetrie der Polarisation schnell aus, wodurch die schwache Wechselwirkung verschwindet und die alleine in den Fordergrund tritt. Dies veranschaulicht geometrisch, warum diese Wechselwirkung nur auf sehr geringe Distanzen wirkt.
Die in der Natur möglichen , welche nur durch die schwache Wechselwirkung vermittelt werden, sind maßgeblich durch die Kombination von äußerem Spin und innerem Spin sowie von der elektrischen Ladung bestimmt. Dies wird im weiteren Verlauf gezeigt.
Ich vermute, dass der schwache Isospin und die sich aus ihm ergebende schwache Ladung eine Spin-Komponente ist, welche aus einer bestimmten, anteiligen Kombination der drei Spins und der Dichteverteilung der Wirkungsquanten(Link) auf dem String des Leptonen-Modells erzeugt wird.
Wie sich der schwache Isospin und die schwache Ladung rechnerisch aus dem Leptonen-Modell ergeben, ist noch nicht abschließend geklärt.
Asymmetrisches Verhalten von rechts- und linkshändigen Teilchen
Bild und/oder Film für die Händigkeit erstellen …
In der Natur wird beobachtet, dass die Stärke der schwachen Wechselwirkung von der Orientierung des äußeren Spins eines Teilchens zu seiner Bewegungsrichtung und der Geschwindigkeit abhängig ist. Sind Bewegung und Spin gleich ausgerichtet, so spricht man von rechtshändigen Teilchen; bei entgegengesetzter Ausrichtung von linkshändigen Teilchen.
Ich vermute, dass im hier beschriebenen Elementarteilchenmodell(Link) die Asymmetrie bei linkshändigen Teilchen je stärker ausgeprägt ist,
desto schneller sie sich bewegen.
Bei rechtshändigen Teilchen ist die Asymmetrie dann je geringer, desto schneller sich die Teilchen bewegen.
Bei den entsprechenden Antiteilchen verhält es sich genau umgekehrt.
Dies ist mit der asymmetrischen Orientierung der verschiedenen Spins untereinander und der Verteilung der dichter besetzten Bereiche im
Wirkungsquanten-String verbunden.
Den Grund für die Veränderung der Asymmetrie durch Bewegung sehe ich in der relativistischen Abflachung (Kontraktion)(Link)
der Struktur des Leptons durch seine Bewegung im Raum (Vakuum).
Diese Vermutung ist in Zukunft mittels Berechnungen und Simulationen zu untersuchen und wäre bei ihrer Bestätigung ein gewichtiger Hinweis auf die Richtigkeit der Quanten-Fluss-Theorie.
Albrecht Giese beschreibt in seinem Basisteilchenmodell einen entsprechenden Ansatz der geometrischen Veränderung von
Wechselwirkungsfeldern, welche sich im Raum bewegen und durch lichtschnelle Wechselwirkungsteilchen (Bosonen) vermittelt werden,
Dieser Ansatz ist vermutlich geeignet, unter Berücksichtigung der speziellen Eigenschaften der Wirkungsquanten,
zur Berechnung der Veränderung der Asymmetrie auf das Leptonen-Modell angewandt zu werden.
Die nahezu absolute Konstanz der Wirkungsquanten-Geschwindigkeit im Raum (Zeit)
bei relativer Verlangsamung der Lichtgeschwindigkeit (Alterung)
entlang der inneren Lichtbahn des bewegten Elementarteilchens hat dabei sicherlich einen gewichtigen Einfluss.
→ Elektrische Ladung — Leptonen-Modell
→ Schwache Ladung — Leptonen-Modell
→
→
→
→ Lösung des ›Problems der Zeit‹ — Leptonen-Modell
| |
Neutrinos |
|
… sind nicht ihre eigenen Antiteilchen
|
Einen Film erstellen …
Die Neutrinos, die Leptonen, haben im Leptonen-Modell eine Struktur, die bei sechs hypothetischen Phasen ebenfalls aus sechs elektrischen, dichter gepackten Polarisationspolen besteht. Ihre Struktur besitzt aber doppelt so viele Wellen wie bei geladenen Leptonen – also zwölf. Dadurch sind im Verlauf einer Phase alle zwölf Pole, sowohl die sechs mit minimaler, als auch die sechs mit maximaler Dichte, gleichzeitig nach außen oder nach innen gerichtet.
Durch die asymmetrische Verteilung und Rotation der Pole tragen Neutrinos eine . Aufgrund der im aufgezeigten des Elementarteilchenmodells(Link) zählen die Neutrinos zu den Antiteilchen und die Anti-Neutrinos zu den Teilchen.
Nach dem Leptonen-Modell der Quanten-Fluss-Theorie ist ein Neutrino nicht sein eigenes Antiteilchen. Ein Neutrino und sein Anti-Neutrino sind unterschiedlich, weil sie einen entgegengesetzten tragen. Ein Hinweis, dass dies den bisherigen Experimentellen befunden entspricht ist, dass bisher kein neutrinoloser Doppelbetazerfall beobachtet wurde, der durch andere Experimente bestätigt werden konnte.
Dies ist ein Indiz für die Richtigkeit der Quanten-Fluss-Theorie.
→
→ Leptonen-Modell
→
→
→ Antiteilchen — Leptonen-Modell
→ Neutrinos — Leptonen-Modell
| |
Quarks |
|
… sind den Leptonen ähnliche Teilchen mit einem gewissen Unterschied
Die von der elektroschwachen Wechselwirkung ebenfalls betroffenen Quarks funktionieren im Elementarteilchenmodell der Quanten-Fluss-Theorie im Wesentlichen wie die Leptonen. Bei ihnen handelt es sich allerdings nicht um vollständig geschlossene Wirkungsquanten-Strings. Aus diesem Grund sind Quarks immer zu vollständigen und ganz geschlossenen Strings miteinander verbunden – den Hadronen(Link) (drei Quarks) oder den Mesonen(Link) (zwei Quarks). Dies kommt, weil die Quanten-Fluss-Theorie nur geschlossene Strings kennt.
In Arbeit …
Hier beschreiben, dass die Strings von Hadronen und Mesonen Sprünge in ihrem Rotationszustand um die Lichtbahn besitzen, welche den Gluonen(Link) entsprechen … Bei Hadronen sind es Sprünge von einer Drittelrotation, bei Mesonen um eine Halbrotation. Die Gluonen sehen also wie ein Teil-String eines Photons oder Elapsons aus. Weil am Ende immer eine ganze Rotation um die Lichtbahn herauskommen muss, müssen entsprechend viele Quarks im String sein. Die Gluonen tragen dann den passenden Farbladungsübergang.
Daraus ergibt sich auch das Confinement …
| |
Symbolismus |
|
Kategorisierung der Elementarteilchen
In den Teilchen des Elementarteilchenmodells der Quanten-Fluss-Theorie, welche Ruhemasse besitzen, steht der innere Spin in einer festen, relativen Orientierung zum normalen äußeren Spin des Teilchens. Beim entsprechenden Antiteilchen ist die relative Orientierung des inneren Spins entgegengesetzt. Ebenso trägt die das umgekehrte Vorzeichen.
|
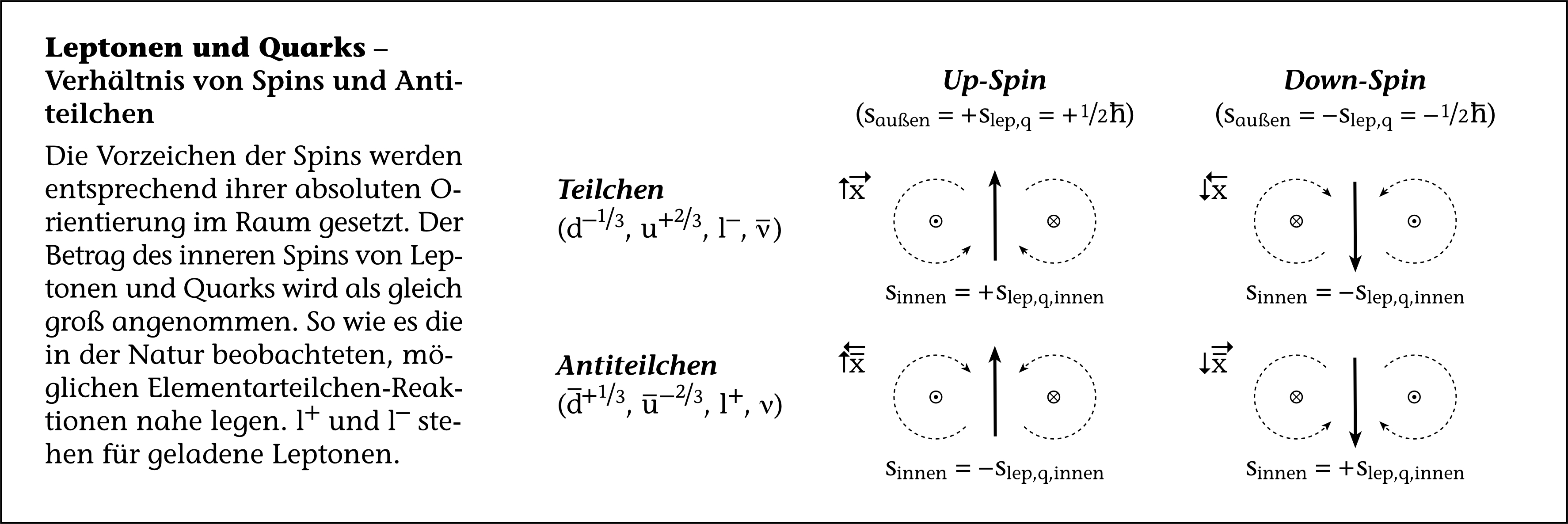
Die ordnet die Orientierungen und die Vorzeichen der Spins den Teilchen und Antiteilchen in einer Konvention zu. Dabei gibt es die dort dargestellten, folgenden Möglichkeiten:
\( \mathrm{\uparrow}\overset{\rightarrow}{x} \), \( \mathrm{\downarrow}\overset{\leftarrow}{x} \), \( \mathrm{\uparrow}\overset{\leftarrow}{\overline{x}} \) und \( \mathrm{\downarrow}\overset{\rightarrow}{\overline{x}} \).
Die vertikalen Pfeile \( \downarrow \) und \( \uparrow \) stehen für den negativen (down) und positiven (up) äußeren Spin.
Die horizontalen Pfeile \( \leftarrow \) und \( \rightarrow \) stehen für den negativen (backward) und positiven (forward) inneren Spin.
Die Orientierungen der Rotationen sind absolut im Raum definiert.
Bei der ersten und der zweiten Variante handelt es sich um das gleiche Teilchen, welches im Raum um 180° gedreht ist.
Die dritte und vierte Variante ist das dazugehörige Antiteilchen – durch den Balken gekennzeichnet –,
deren Varianten ebenfalls zueinander gedreht sind.
Ich folgere, dass es in der Quanten-Fluss-Theorie eine objektive Kategorisierung von Teilchen und Antiteilchen gibt, welche durch die Spin-Kombinationen festgelegt ist: Tragen äußerer und innerer Spin das gleiche Vorzeichen, dann ist es ein Teilchen. Tragen beide das entgegengesetzte Vorzeichen, dann handelt es sich um ein Antiteilchen.
Die werden in der Quanten-Fluss-Theorie anders kategorisiert als in der heute gültigen Lehrmeinung:
In der Quanten-Fluss-Theorie ist bezüglich der Spin-Kombinationen zu beachten, dass die Neutrinos zur Kategorie der Antiteilchen und die Anti-Neutrinos zur Kategorie der Teilchen gerechnet werden.
Dies kann etwas Verwirrung stiften.
→ Spins — Leptonen-Modell
→ Antiteilchen — Leptonen-Modell
→
→
| |
Teilchenumwandlungen |
|
Transmutationen der Elementarteilchen
(• Hier auch den Myonen-Zerfall beschreiben?)
Um die Teilchenumwandlungen darzustellen werden im Folgenden die Teilchenzusammensetzungen von Proton p+ und Neutron n, nach den heute gültigen Erkenntnissen aus jeweils drei bestehend, aufgelistet. Die hochgestellten Zahlen geben die an:
|
|
(Esw.1) |
|
|
(Esw.2) |
Bei Teilchenreaktionen ist auch die Energiebilanz zu berücksichtigen. Dabei steckt sowohl Energie in der Teilchenbewegung, als auch sogenannte Ruheenergie in der Teilchenstruktur. Zusätzlich kann Energie in Form von Lichtteilchen (Photonen) vorhanden sein.
Nur die schwache Wechselwirkung ist in der Lage Teilchenumwandlungen zu vermitteln. Der Beta-Zerfall eines Neutrons n in ein Proton p+ beispielsweise stellt sich dann, mit dem Zwischenprodukt eines elektrisch negativ geladenen W−-Bosons sowie der möglichen Erzeugung eines linear polarisierten Photons γ, wie folgt dar:
|
|
(Esw.3) |
|
|
(Esw.4) |
|
|
(Esw.5) |
Dabei bleiben sowohl der normale, äußere (↓,↑) als auch der innere Spin (Drehimpuls) (←,→) in ihrer Summe erhalten. Das heißt, die Anzahl der Pfeile in der jeweiligen Richtung und entgegengesetzt dazu, passen auf beiden Seiten der Reaktion zueinander. Dies gilt ebenso für die Summe der elektrischen Ladungen und die Summer der Energien. Zu beachten ist weiterhin, dass Quarks nur in dreier oder zweier Verbünden, den Hadronen oder Mesonen, vorkommen.
Die Umwandlung eines Neutrons n in ein Proton p+ wird im Quark-Modell auch als die Umwandlung eines Down-Quarks d in ein Up-Quark u verstanden:
|
|
(Esw.6) |
|
|
(Esw.7) |
Hierbei ist allerdings folgende Festlegung der Quanten-Fluss-Theorie zu beachten:
Alle Fermionen, wie Leptonen, Quarks und Hadronen, besitzen vom Betrag her den gleichen inneren Spin sfer,innen. Sein Betrag ist nach der folgenden Formel von der bisher nicht bekannten Leptonen-Phasenzahl abhängig (Diese Formel gibt aus schon auf der Leptonen-Seite. Deren Nummer hier benutzen und mit einem Link versehen.):
|
|
(Esw.8) |
Dieser Spin unterliegt einer globalen Erhaltung.
Interessant ist nun die Frage, ob das W−-Boson nach dem Teilchenmodell der Quanten-Fluss-Theorie noch in andere Varianten der gleichen Leptonen zerfallen kann. Dies würde nicht mit den Beobachtungen in der Natur übereinstimmen. Fest steht, dass es kein Positron e+ – also ein positiv geladenes Elektron-Antiteilchen – sein kann. Dies würde die Ladungserhaltung verletzen. Denkbar wäre ein Elektron und dazu ein gedrehtes Anti-Neutrino, ein Neutrino oder gedrehtes Neutrino anstatt des Anti-Neutrinos:
|
|
(Esw.9) |
|
|
(Esw.10) |
|
|
(Esw.11) |
|
|
(Esw.12) |
|
|
(Esw.13) |
|
|
(Esw.14) |
|
|
(Esw.15) |
Es gibt allerdings nur noch eine weitere Spin-Kombination, welche zum Zerfall
eines W−-Bosons passt.
Diese ist der Zerfall
eines um 180° gedrehten W−-Bosons.
Hier zerfällt das Boson in die gleichen, ebenfalls um 180° gedrehten Leptonen.
Es handelt sich folglich um die gleiche Zerfallsreaktion.
Als Zerfallsprodukte kommen ansonsten noch die anderen Generationen
der jeweils entsprechenden Leptonen-Familien,
in betracht, welche die gleichen Spin-Kombinationen und Ladungen tragen.
Jedenfalls soweit dies energetisch möglich ist.
Ich folgere, dass der Beta-Zerfall im Teilchenmodell der Quanten-Fluss-Theorie nur wie oben geschildert ablaufen kann. Dies kommt, weil sowohl der äußere und der innere Spin beim W−-Boson das gleiche Vorzweichen tragen. Insbesondere kann dieses Boson nicht in ein bezüglich der Ladung passendes Neutrino anstatt des Anti-Neutrinos zerfallen.
Es zeigt sich also, dass das Elementarteilchenmodell der Quanten-Fluss-Theorie die Teilchenumwandlungen bemerkenswert gut darstellen kann.
Das einzige andere Boson, welches auch noch eine Teilchenumwandlung vermitteln kann ist das Antiteilchen von W−, das W+-Boson. Bei diesem Boson ist entweder nur der äußere oder nur der innere Spin umgekehrt. Daher kann dieses nur in die Anti-Leptonen des W−-Zerfalls oder deren 180° Drehungen zerfallen:
|
|
(Esw.16) |
Die beiden übrigen Bosonen der elektroschwachen Wechselwirkung, das Photon γ und das Z0-Boson, vermitteln keine Teilchenumwandlungen. Das Photon zerfällt gar nicht und das Z0-Boson zerfällt nur in Teilchen-Antitielchen-Paare. Das können sowohl elektrisch neutrale oder elektrisch geladene Teilchen sein, wie beispielsweise:
|
|
(Esw.17) |
Das Z0-Boson kann also nicht am Beta-Zerfall beteiligt sein.
→
→
→ Spins — Leptonen-Modell
→
→ Familien und Generationen — Leptonen-Modell
| |
Fußnoten |
|
| 1. |
Vgl. Wikipedia, Elektroschwache Wechselwirkung. Vgl. Fritzsch, Mikrokosmos, 6. Kap. Elektroschwache Wechselwirkungen, S. 105-118. | |
| 2. | Vgl. Wikipedia, Isospin, Erweiterung auf schwachen Isospin. | |
| 3. | Eine genaue Herleitung, ob die mit Wirkungsquanten dichter gepackten Stellen des Strings einer positiven oder negativen elektrischen Polarisationen des elektrischen Feldes entsprechen, wird gesucht. Die Asymmetrie der könnte hier weiter helfen. Hinweise darauf sind erbeten. | |
| 4. | Vgl. Wikipedia, Schwache Wechselwirkung. | |
| 5. | Vgl. Wikipedia, Isospin, Erweiterung auf schwachen Isospin. | |
| 6. | Eine genaue Herleitung, wie sich die schwache Isospin-Komponente aus den drei Spins und der elektrischen Polarisation des Leptonen-Modells ergeben, wird gesucht. Hinweise darauf sind erbeten. | |
| 7. | Vgl. Wikipedia, Weak interaction, Violation of symmetry. | |
| 8. | Eine genaue Herleitung oder Berechnung der Veränderung der Asymmetrie wird gesucht. Hinweise darauf sind erbeten. | |
| 9. | Giese, Relativistic Contraction without Einstein!. | |
| 10. |
Vgl. Fritzsch, Mikrokosmos, 7. Kap. Oszillierende Neutrinos, S. 119-127. Vgl. Wikipedia, Neutrino. | |
| 11. | Vgl. Wikipedia, Doppelter Betazerfall, Neutrinoloser Doppel-Betazerfall. | |
| 12. | Vgl. Göger-Neff, »Große Geheimnisse um kleine Teilchen«, S. 53. | |
| 13. |
Vgl. Fritzsch, Mikrokosmos, 4. Kap. Quarks, S. 69-76, 5. Kap. Quarks mit Farbe, S. 77-103. Vgl. Wikipedia, Quark (Physik). | |
| 14. |
(Primärliteratur einfügen!) Internet: Vgl. Max Planck Institute for Gravitational Physics, »Ruhemasse«. Vgl. Wikipedia, Masse, Spezielle Relativitätstheorie, Ruhemasse. | |
| 15. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Myon, Zerfall. | |
| 16. | Vgl. Wikipedia, Baryon, Baryon-Multipletts, Das Baryon-Oktett. | |
| 17. | Vgl. Wikipedia, Weak interaction, Interaction types, Charged current interaction. | |
| 18. | Vgl. Wikipedia, Weak interaction, Interaction types, Charged current interaction. | |
| 19. | Vgl. Beringer, Particle Physics Booklet, Z, S.9-10, hier S. 9. |
| |
Stand 29. Februar 2024, 17:00 CET.
-
Permanente Links:
(Klicke auf die Archivlogos
zum Abruf und Ansehen
der Archive dieser Seite.) -

-
archive.todaywebpage capture