| ← |
Quantengravitation und Higgs-Mechanismus — Neue Physik |
Quantengravitation der Elementarteilchen
Die Gravitation der Allgemeinen Relativitätstheorie offenbart sich als emergentes Phänomen der Beugung lichtähnlicher Strukturen in einem Modell von Elementarteilchen-Strings neuer Art
Rotierende Impulskegel der neuen Feinstruktur der gravitativ wirkenden Elementarteilchen-Strings einer Zentralmasse verlangsamen und beugen die Bewegung lichtähnlicher Strukturen in ihrem Umfeld und führen so zur Quantengravitation
| ▾ | Notizen |
Wirkungsquanten-Impulskegel
• Untersuchen, wie sich bei steigender Gravitation und damit verringerndem Gang der Spiralbahnen die Wirkungsquanten-Impulskegel der Vakuum-Elapsonen in deren String in ihrer Lage verändern:
– Verändern sich die Impulskegel in ihrer Geometrie?
⋅ Das tun sie, meiner Meinung nach. Die Impulskegel verlassen die Wirkungsquanten auf ihrer Strukturebene zunächst im 45° Winkel mit √2 (1,41-facher) Lichtgeschwindigkeit. Treffen sie auf die umgebende Struktur des Vakuums und seiner unpolarisierten Photonen, dann wird der Impuls auf diese Strukturen übertragen, dabei ständig abgelängt und pflanzt sich auf der Strukturebene der Elementarteilchen effektiv nur mit Lichtgeschwindigkeit fort.
– Wie ist dieses Einklappen mit der Detektorwellenlänge der Vakuum-Elapsonen im Vakuum korreliert?
– Was passiert dabei am Ereignishorizont eines Schwarzen Lochs? Ragen die Kegel in das Schwarze Loch hinein?
Gravitonen
• Sind die Vakuum-Elapsonen die Gravitonen? Bisher nach meiner Ansicht eher nicht, weil Vakuum-Elapsonen Spin 1 haben sollten und die Gravitonen Spin 2.
• Die Wirkungsquanten tragen den Spin 2, wie die Gravitonen, wenn ich es richtig sehe.
• Weitere Gedanken zu den Gravitonen finden sich in der Einleitung unter Hypothese: Das Vakuum und wie es die Wechselwirkungen vermittelt.
Aktuelle Fachdiskussion
• Die Quantenmechanik ist emergent: Tim Palmer bringt in seinem Beitrag die Unentscheidbarkeit, die Unberechenbarkeit und die Vereinheltichung der Physik zusammen. Er führt darüber die Quantenphysik, die Relativitätstheorie und die Chaos-Theorie näher aneinander heran. Guest Post: “Undecidability, Uncomputability and the Unity of Physics. Part 1.” by Tim Palmer
• Wie können wir feststellen, ob die Gravitation quantisiert ist? Und wofür ist das wichtig? Siehe: Ein Stück Schwerkraft. In: Spektrum der Wissenschaft 08/2018. 18-22.
Die Erklärung der Gravitation in Form der Quantengravitation ist eine der sehnlichsten Wünsche der heutigen theoretischen Physik.(Verweis auf Hossenfelder Blog und SdW) Sie steht im Zentrum der Vereinheitlichung der Physik, der Verschmelzung von Quantenphysik (Quantenfeldtheorie) und Allgemeiner Relativitätstheorie, von der sich viele Physiker das Verständnis mancher bisher unerklärlicher Beobachtungen und wichtiger Fragen erhoffen.
|
Notwendige Konkretisierung der Lehrmeinung ⚠️
Bevor ich zur Vorstellung der Mechanismen und deren Details komme, möchte ich noch einmal kurz darauf hinweisen, dass es einer Konkretisierung der Lehrmeinung bedarf, um sich aus heutiger akademischer Perspektive auf die anschließend beschriebene physikalische Perspektive seriös einzulassen. Die notwendige Konkretisierung der Lehrmeinung beschreibe ich in der Einleitung und lege die Annahmen, die meiner neuen Perspektive zugrunde liegen, auf der Seite First-Principles dar.
Mehrere Mechanismen führen zur Gravitation
Eine Kette von aufeinander aufbauenden Mechanismen liefert uns das Verständnis dafür, wie die Quantengravitation zustande kommt. Für den Überblick der Mechanismen, die hier am Wirken sind, beginne ich die Beschreibung beim Elementarteilchen, das angezogen wird, und ende mit dem Ausgangspunkt, dem Ursprung, dieser Kette.
Bei der anschließenden detaillierten Beschreibung beginne ich dann in umgekehrter Reihenfolge …
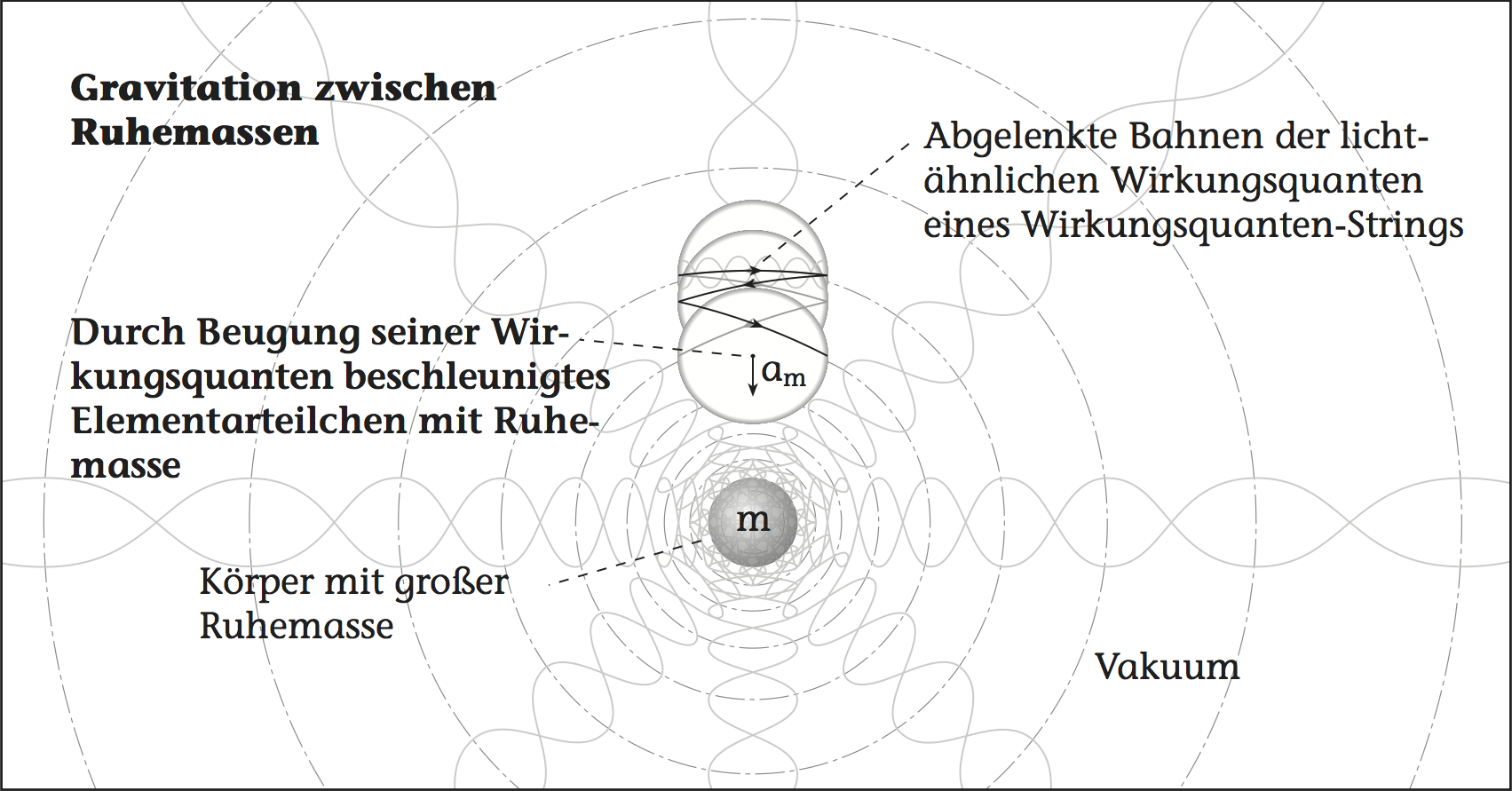
Eine Beugung von lichtähnlichen Strukturen in Elementarteilchen beschleunigt diese – Lichtablenkung
Die veranschaulicht, grob vereinfacht, eine anziehende Zentralmasse m und
die umgebenden Verhältnisse im Vakuum des neuen Modells, auf die ich gleich noch weiter eingehe.
|
Oberhalb der anziehenden Zentralmasse befindet sich ein schematisches Elementarteilchen des Modells, in dem lichtähnliche Strukturen zirkulieren (detaillierter in ). Diese lichtähnlichen Strukturen werden, wie von Lichtteilchen (Photonen) in der Allgemeinen Relativitätstheorie bekannt, zur zentralen Masse hin abgelenkt. Ihre Bahn ist also gebeugt. Die Beugung der in ihnen zirkulierenden Strukturen führt zu einer Beschleunigung des angezogenen Elementarteilchens in Richtung der Masse, die der bekannten Gravitation entspricht.
Die Beugung lichtähnlicher Strukturen kommt durch deren Verlangsamung im Gravitationsfeld zustande – Shapiro-Verzögerung
Die angesprochene Beugung von Licht, oder von dem Licht ähnlichen Strukturen, ergibt sich dadurch, dass deren Ausbreitungsgeschwindigkeit im dreidimensionalen Raum
auf der der Masse zugewandten Seite langsamer ist, als auf der von ihr abgewandten Seite (siehe ).
Die Verlangsamung lichtähnlicher Strukturen wird durch eine Störung der Lichtbewegung verursacht – Undulation der Lichtbahn
Anders als in der Allgemeinen Relativitätstheorie wird die Verlangsamung des Lichts, oder ähnlicher Strukturen, durch eine
wellenförmige Störung seiner Ausbreitungsbahn verursacht und nicht direkt durch die Krümmung des Raums oder der Raumzeit.
Diese wellenförmige Störung der Lichtbahnen, und vergleichbarer Bahnen lichtähnlicher Strukturen des Vakuums in der Umgebung einer Masse, bringt allerdings unterschiedliche Energiedichten des Vakuums hervor, die als Raumzeitkrümmung erscheinen (siehe , wellenförmige Erscheinungen im dem Vakuum eingeprägten Gravitationspotenzial; Energiedichtegradient als Gradient der De-Broglie-Frequenz oder De-Broglie-Wellenlänge).
|
Die wellenförmige Störung der Lichtbahn hat ihre Ursache in den rotierenden Impulskegeln der Feinstruktur der Elementarteilchen der gravitativen Masse
Die gravitativ anziehende Masse besteht aus Elementarteilchen.
Die Feinstruktur dieser Elementarteilchen besteht aus Wirkungsquanten (siehe ).
Auch deren Wirkungsquanten strahlen Impulskegel in den Raum ab (siehe ),
wie sie in dargestellt sind.
Die Impulskegel treffen auf Licht oder dem Licht ähnliche Strukturen in ihrer Umgebung und stören deren Bahn wellenförmig (siehe ), was deren Verlangsamung zur Folge hat.
Erst die Berücksichtigung der statistischen Verteilung dieser Störung bringt das korrekte Ergebnis hervor
Analysieren wir die Lichtverlangsamung, die ein einzelnes Elementarteilchen durch seinen gravitativen Effekt in der Umgebung verursacht,
dann erhalten wir nicht die Lichtverlangsamung, die beobachtet und in der Allgemeinen Relativitätstheorie vorhergesagt wird.
Erst viele in einer Zentralmasse versammelte Elementarteilchen bringen die korrekte Lichtverlangsamung im 3-dimensionalen Raum hervor. Nämlich dann, wenn wir verstehen, dass das Zusammenspiel der wellenförmigen Störungen vieler Elementarteilchen einem statistischen Effekt unterliegt.
Quanten der Gravitation bisher unbeobachtet?
Ein Perspektivwechsel
Bisher gehen wir in der akademischen Physik davon aus, dass wir keine Phänomene beobachten, die einen direkten Rückschluss auf die Quanten der Gravitation zulassen. Ich bin mittlerweile durch die neue Physik der Quanten-Fluss-Theorie zu dem Schluss gekommen, dass dies nicht stimmt.
Die zuvor eingeführte ›Abzählinterpretation der Heisenbergschen Unschärferelation‹ bedeutet in meinen Augen, dass die Elementarteilchen Wirkungsimpulse h (Plancksches Wirkungsquantum) als Impulskegel abstrahlen (siehe ), die wir bei ihrer Energie- oder Impulsmessung beobachten und pro Zeit- oder Längeninterval zählen.
Genau diese Impulse sind jedoch auch, wie bereits erwähnt und nachfolgend detailliert beschrieben, die Ursache der gravitativen Lichtverlangsamung (gravitative Zeitdilatation) und Lichtbeugung, die schließlich, aufgrund der neuen Elementarteilchen-String-Struktur, zur Gravitation führen (siehe ).
So gesehen beobachten wir die Impulse der Quanten der Gravitation längst als Plancksches Wirkungsquantum, haben sie aber bisher nicht als solche erkannt. Hieran wird wunderbar sichtbar, wie entscheidend Interpretationen und ihre Perspektivwechsel dafür sein können zu beurteilen, was wir schon längst in Händen halten.
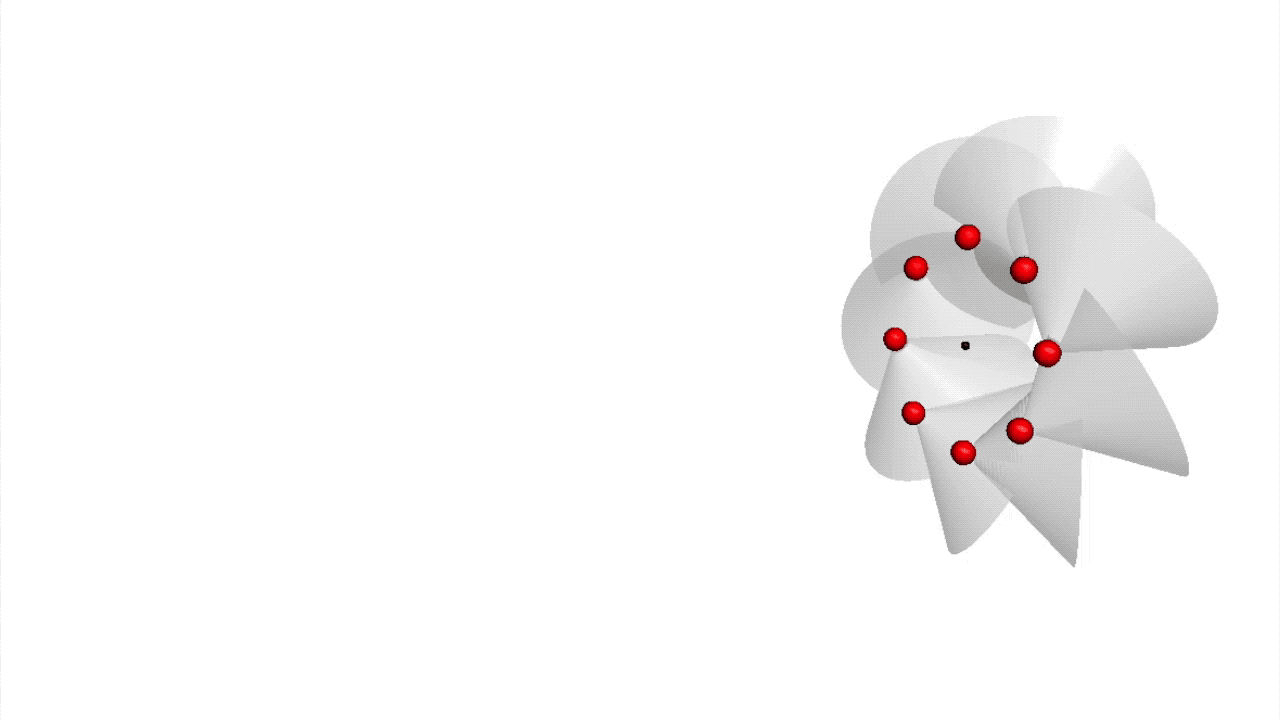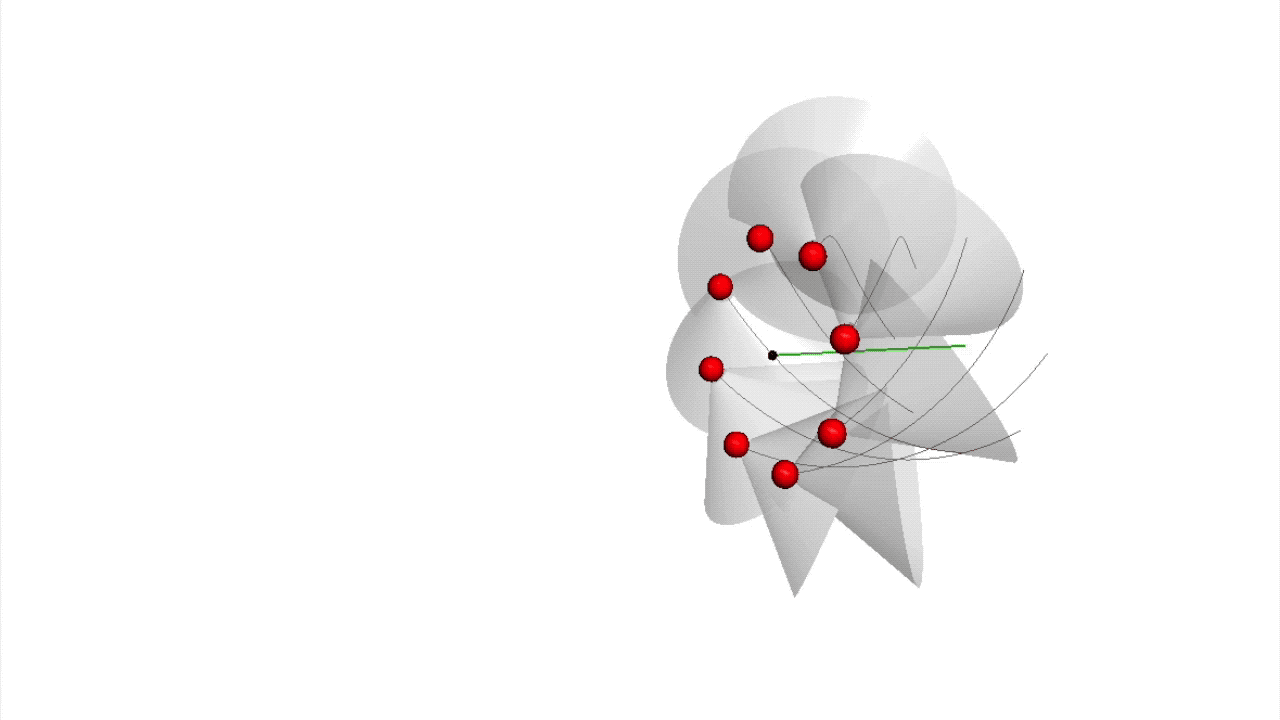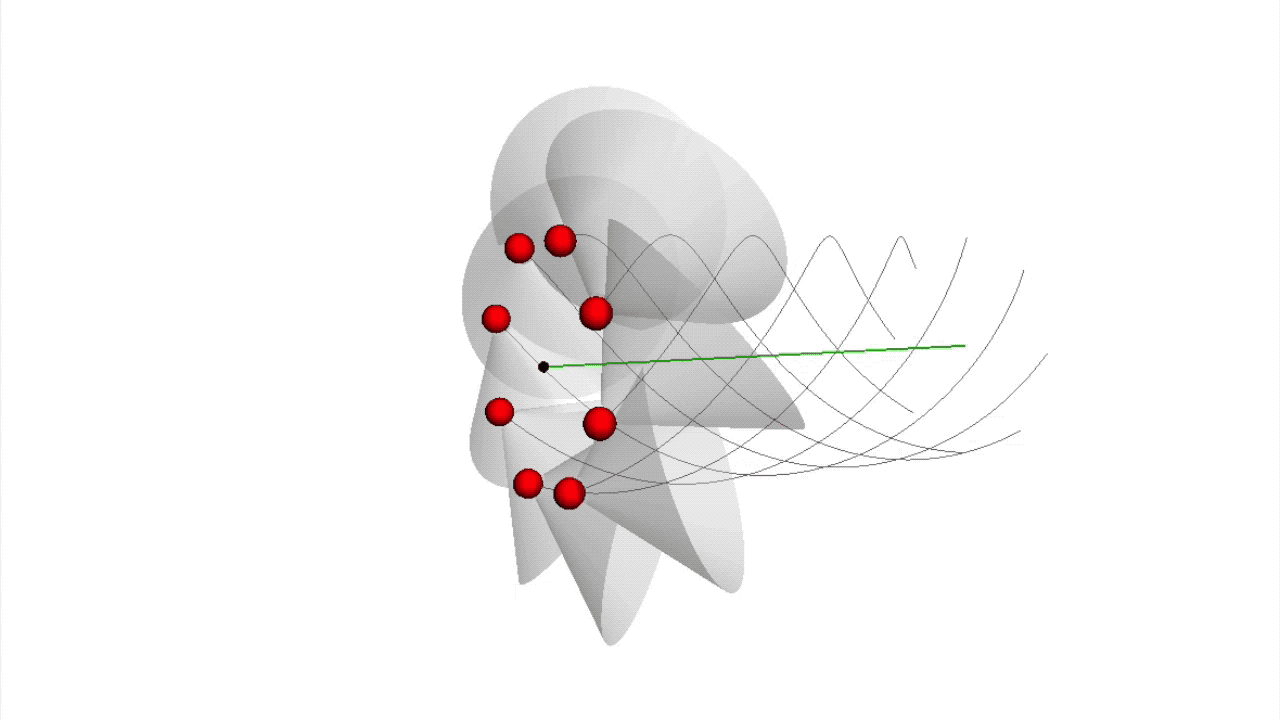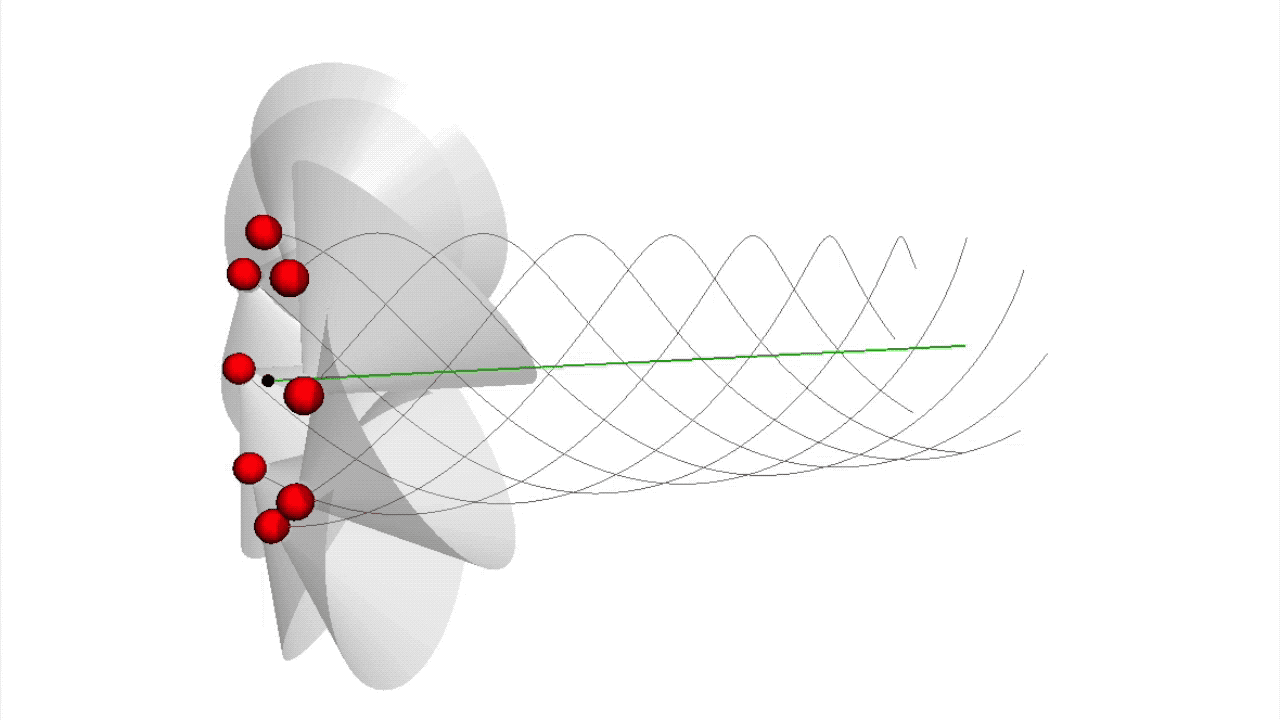
Durch die ›Abzählinterpretation der Heisenbergschen Unschärferelation‹ wird das Plancksche Wirkungsquantum zum neuen Fundamentalteilchen, zum Wirkungsquant wq (siehe rote Kugeln in und ). Diese Wirkungsquanten fügen sich zu den Elementarteilchen-Strings der Quanten-Fluss-Theorie zusammen.
Die von den Wirkungsquanten abgestrahlten Impulskegel in , die entsprechend auch die Wirkungsquanten in verbinden (nicht eingezeichnet), lösen in benachbarten Elementarteilchen-Strukturen die gravitative Anziehung aus, wie auf dieser Seite gezeigt wird.
Graviradiation
Die Vereinheitlichung der Physik durch eine neue, fundamentale Wechselwirkung
Alle uns bekannten Wechselwirkungen sind im mikroskopisch Kleinen auf die neue Wechselwirkung der von mir sogenannten Graviradiation zurückzuführen.
Über diese, der ganzen Physik zugrundeliegende Wechselwirkung liefert die Quanten-Fluss-Theorie einen Mechanismus der einen Ansatz zur Vereinheitlichung der Quantenphysik mit der Allgemeinen Relativitätstheorie bietet.
Graviradiation – Eine neue Wechselwirkung
Ich nenne diese Wechselwirkung Graviradiation.
Sie wird durch die Wirkungsquanten-Impulskegel – – vermittelt, die jedes Wirkungsquant aussendet.
Quantenphysik
Die Graviradiation ist dafür ursächlich, dass die Genauigkeit unserer Beobachtung auf die Heisenbergsche Unschärferelation beschränkt ist,
wie ihre Abzählinterpretation deutlich macht.
Vakuum- und Elementarteilchen-Struktur
Sie ist dafür verantwortlich, dass sich die Bahnen der Wirkungsquanten zu Helixspiralen aufwickeln und zu Elementarteilchen-Strings verbinden (siehe und ).
So zeigt sich dann auch die Struktur des Vakuums idealisierter Weise als aus unpolarisierten Photonen bestehend.
Auch führt sie über seine innere Wechselwirkung dazu, dass das Vakuum – der Raum und die Zeit – seine stabile Dimensionierung erhält. Dies wird näher auf der Seite Emergente Gravitation ergründet.
Gravitation
Nicht zuletzt ist sie, wie schon gesagt, für die Emergenz der Quantengravitation verantwortlich.
Phänomen der Dunklen Materie
Über die Vakuum-Struktur und deren innere Wechselwirkung, durch das in ihr in Form von ungleich verteilter Vakuum-Energiedichte „eingravierte“ Gravitationspotenzial,
ist die Graviradiation auch für das
der weit im Raum verteilten, sehr großen Massenansammlungen verantwortlich, wie sich zeigt.
Ansatz der Quantengravitation
Die nachfolgend in erster Näherung hergeleitete ortsübliche Lichtgeschwindigkeit im dreidimensionalen Raum des äußeren Gravitationsfelds einer homogenen Massenkugel entspricht genau der äußeren Schwarzschild-Metrik als Lösung der Allgemeinen Relativitätstheorie.
Der verwendete Ansatz zur quantitativen Beschreibung der Quantengravitation stammt aus dem Basisteilchenmodell von Albrecht Giese und verfeinert diesen mit Hilfe der Elementarteilchen-Struktur der Quanten-Fluss-Theorie.
Im Zentrum von Gieses Überlegung steht die Idee, dass ein Elementarteilchen, welches eine innere Struktur hat und aus rotierenden, lichtähnlichen Basisteilchen aufgebaut ist, in seine Umgebung aussendet. Diese Störungswellen verlängern den Bewegungspfad von Lichtteilchen – Photonen – oder den der lichtähnlichen Strukturen in anderen Elementarteilchen in ihrem Umfeld. Auf diese Weise und sich die Bewegung lichtähnlicher Strukturen im Raum, der eine gravitative Masse umgibt. Befinden sich also Materie-Elementarteilchen in der Umgebung, bewegen diese sich auf die anziehende Masse zu, weil sie nach Giese ja aus lichtähnlichen Basisteilchen bestehen.
In der Quanten-Fluss-Theorie werden Gieses Basisteilchen nun durch Wirkungsquanten ersetzt, die zu geschlossenen Strings verbunden sind. Die Störungswellen sind die Wirkungsquanten-Impulskegel (virtuelle Wirkungsquanten) der neuen Graviradiation. Die Quanten-Fluss-Theorie verfeinert also seinen Ansatz durch das neue Modell der Elementarteilchen aus Wirkungsquanten-Strings, wie zum Beispiel bei Leptonen (siehe ). Durch die hier entwickelten Details werden auch Eigenschaften von Gieses Erklärungsansatz verständlich, die für mich bei ihm offen bleiben.
| → |
|
Vereinfachtes Modell der Quantengravitation |
|
Wirkungsquanten-Impulskegel wirken als Störungswellen
| ← |
|
Die nachfolgenden Erklärungen werden aus Sicht eines kosmischen Beobachters beschrieben.
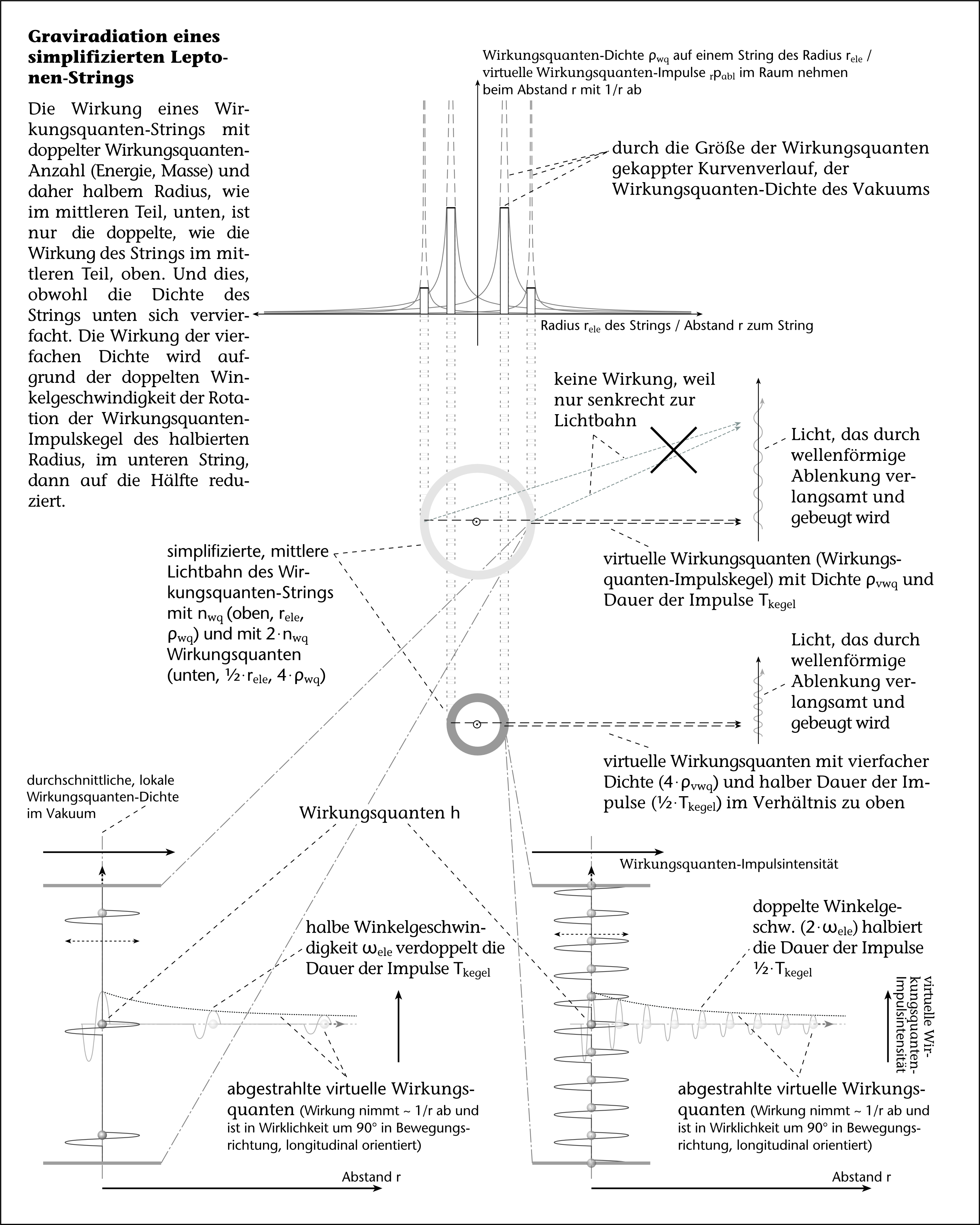
Vereinfachter Wirkungsquanten-String
Ein kreisförmiger Ring aus Wirkungsquanten
Vereinfachen wir den Wirkungsquanten-String eines Materie-Elementarteilchens, so können wir uns diesen als Ring aus Wirkungsquanten vorstellen, welcher mit Lichtgeschwindigkeit rotiert (siehe , obere und untere Mitte). Die Wirkungsquanten eines solchen, simplifizierten Strings strahlen durch ihre Wirkungsquanten-Impulskegel Störungswellen in Form von Impulsen senkrecht zum Ring in ihr Umfeld ab, von mir virtuelle Wirkungsquanten genannt (siehe , unten).
Die virtuellen Wirkungsquanten sind als Dichtewellen in den Wirkungsquanten des Bewegungsraums der Quanten-Fluss-Theorie zu verstehen. Diese vermitteln die neue Wechselwirkung der , was bedeutet, dass sie die makroskopische Geschwindigkeit anderer Wirkungsquanten in ihrem Umfeld durch eine wellenförmige Ablenkung (Undulation) verringern und deren Bahn oft auch insgesamt ablenken, wie wir sehen werden (siehe , links).
Warum Impulskegel?
Wie Giese an anderer Stelle in seinem Basisteilchenmodell ausführt, verändert sich die räumliche Geometrie der Ausbreitung von lichtschnellen Wechselwirkungsteilchen, wenn das abstrahlende Teilchen sich bewegt. Die Veränderung vollzieht sich dabei in Abhängigkeit von der Bewegungsgeschwindigkeit so, dass sich das abgestrahlte Feld in Bewegungsrichtung umso mehr abflacht, also von der Kugel zum sogenannten Heaviside-Ellipsoid verformt, je größer die Geschwindigkeit ist. Dies entspricht der Lorentzkontraktion (Längenkontraktion) der Relativitätstheorie.
Erreicht das abstrahlende Teilchen Lichtgeschwindigkeit, wie die simplifizierten Wirkungsquanten im vereinfachten Elementarteilchen-String, dann werden effektiv nur noch Wechselwirkungsteilchen senkrecht zur Bewegungsrichtung ausgesandt. Deutlich wird dies auch an folgender Überlegung:
Flacht sich die Struktur eines Elementarteilchens immer weiter ab, dann bewegen sich die Wechselwirkungspole, die für den Zusammenhalt seiner Struktur sorgen, immer weiter in die zentrale Ebene senkrecht zu seiner Bewegungsrichtung. Sind diese Pole nun so gut wie auf dieser Ebene angekommen, dann können sich die Wechselwirkungsteilchen zwischen ihnen auch nur in dieser Ebene und auf diese Weise dann auch nur in Richtung dieser Ebene in den Raum hinaus bewegen.
Dies bedeutet eine zur Bewegungsrichtung der Wirkungsquanten senkrechte und zu jedem Zeitpunkt ringförmige Abstrahlung ihrer Wechselwirkungsteilchen in den Raum.
So ergibt sich dann die Form eines Impulskegels für die Abstrahlung der Wirkungsquanten:
Eine senkrechte Ringform der Abstrahlung der virtuellen Wirkungsquanten je Zeitpunkt heißt eine kegeloberflächenförmige Struktur ihrer Ausbreitung um die Bahn des Strings in der Zeit. Und dieser Kegel hat einen Öffnungswinkel von 90°, denn das abstrahlende Teilchen hat die gleiche Geschwindigkeit, wie seine Abstrahlung.
Dementsprechend hat dann auch das von einem einzelnen Photon, einem Lichtteilchen, abgestrahlte elektromagnetische Feld im zeitlichen Verlauf die Form einer Kegeloberfläche.(Verweis)
Wirkungsquanten-Impulse verringern ihre Intensität im Raum mit $ \frac{ 1 }{ r } $
| ▾ | Notizen |
• Die gute Beschreibung, die an anderer Stelle entfernt wurde, hier einbauen:
– Ungewöhnlicherweise nimmt die Impulsintensität rii der störenden Wirkung der Wirkungsquanten-Impulskegel bei größerem Abstand umgekehrtproportional zum Abstand r vom String ab. Dieses Phänomen entsteht, weil die Impulskegel der Wirkungsquanten ringförmig abgestrahlt werden und sich im Verlauf der Zeit zu einem Impulskegel formen (siehe ).
Die Abnahme ihrer Impulsintensität im Raum hat bei Wirkungsquanten-Impulsen eine Besonderheit:
Eine ringförmige Ausbreitung bedeutet, eine Abnahme der Impulsintensität zum String mit 1/r. Das kommt, weil die Dichte der Wechselwirkungsteilchen im Ring mit 1/r zum String abnimmt, denn der Umfang des Rings nimmt mit r zu, während die Anzahl der Wechselwirkungsteilchen im Ring gleich bleibt.
Damit verhält sich die Graviradiation anders als alle anderen Wechselwirkungen.
Unterschied von Wechselwirkungen mit der Intensitätsabnahme von 1/r2 zu 1/r
Bei einer Wechselwirkung, deren Stärke mit 1/r2 mit dem Abstand r abnimmt, werden die Wechselwirkungsteilchen zu jedem Zeitpunkt in Form von Kugeloberflächen – sphärisch – in den Raum abgestrahlt. In der laufenden Zeit ergibt sich eine kugelförmige Abstrahlung.
Da dies auch bedeutet, die Abstrahlung erfolgt in alle Richtungen im Raum, wird ein in der Nähe befindliches Objekt quasi zu jedem Zeitpunkt von den Wechselwirkungsteilchen getroffen. Alle bisher bekannten Wechselwirkungen, wie die elektromagnetische, die schwache, die starke und die Gravitation, sind von dieser Art.
Die Wechselwirkung eines einzelnen Wirkungsquants ist anders: Bei seiner Wechselwirkung, deren Stärke mit 1/r zum Abstand r vom String abnimmt, werden die Wechselwirkungsteilchen zu jedem Zeitpunkt in Form von Ringen – im zeitlichen Verlauf kegelförmig – abgestrahlt. Dies bedeutet, die Wechselwirkung wird nicht(!) in alle Richtungen abgestrahlt. Ein in der Nähe befindliches Objekt wird nur von den Wechselwirkungsteilchen getroffen, wenn es zu einem Zeitpunkt vom Kegel gestreift wird.
| → |
|
| |
Lichtverlangsamung |
|
Aus virtuellen Wirkungsquanten bestehende Störungswellen erzeugen die Shapiro-Verzögerung des Lichts
| ← |
|
| ▾ | Notizen |
Grundlage dieser Berechnung
• Darauf hinweisen, dass diese Berechnungen im Rahmen des Wirkungsquanten-Bewegungsraums erfolgen und nicht im Rahmen des Licht-Bewegungsraums. Daher ergibt sich die gravitative Rotverschiebung und Zeitdilatation erst korrekt, wenn das Verhältnis von tangentialer und radialer Lichtgeschwindigkeit im hier verwendeten Wirkungsquanten-Bewegungsraum im Verhältnis zur berücksichtigt wird. Im Licht-Bewegungsraum ist dann in Bezug auf die LG generell p = 0 und in Bezug auf die Rotverschiebung für den tangentialen Fall p = 0 und im radialen Fall p = 1/2 zu setzen, so dass sich die korrekte Rotverschiebungsformel ergibt.
• Der Berechnung liegen die Formeln Eele = h⋅fele und Eele = ħ⋅ωele der Quantenphysik für die Energie eines Elementarteilchens zugrunde.
• Aus der Relativitätstheorie wird allerdings die Allgemeingültigkeit der Formel E = m⋅c2 vorausgesetzt und findet dann natürlich auch Anwendung.
– Die Proportionalität von Energie und Masse ist eine direkte Schlussfolgerung der FrQFT, die sich aus der Annahme (Postulat bzw. Axiom) ergibt, dass Wirkungsquanten sowohl Energieeinheiten als auch Masseneinheiten sind (absolut nur auf der untersten Strukturebene des analysierten Modells)! Dies setzt ein konstantes Verhältnis voraus, welches nach unseren Beobachtungen das Quadrat der Lichtgeschwindigkeit c2 der bekannten Formel E = m⋅c2 ist.(Verweis auf Wikipedia: ›Äquivalenz von Masse und Energie‹, Überblick und Beispiele, Vernichtungsstrahlung. Dies ist keine relativistisch interpretierte Beobachtung, sondern eine quantenphysikalisch interpretierte!)
– Ergibt sich die Formel E = m⋅c2 auch aus der Quantenphysik? Ja, wie gerade bemerkt, bei der Paarvernichtung.
– Könnte Formel E = m⋅c2 auch vermieden werden?
• Diese drei Formeln reichen aus, zusammen mit der Struktur des Elementarteilchen-Modells der FrQFT und gewisser Vereinfachungen dieses Modells zuzüglich einer simplen Näherung für größere Abstände sowie einer statistischen Näherung für größere Massen, um die gravitative Lichtablenkung (Gravitation) eines einzelnen Elementarteilchens und die gravitative Lichtablenkung (Gravitation) einer Zentralmasse aus Elementarteilchen korrekt so herzuleiten, wie diese in der Schwarzschild-Metrik der Allgemeinen Relativitätstheorie beschrieben ist.
Mit Raimund Welsch zu klärende Fragen
• Ist die Standardabweichung wirklich das, was hier im Moment angewendet wird?
• Wenn ja, warum darf die Standardabweichung hier angewendet werden?
Hinweise
• Eine Herleitung der Lichtverlangsamung findet sich auch in Variable Lichtgeschwindigkeit in der Allgemeinen Relativitätstheorie, siehe auch Datei "Variable Lichtgeschwindigkeit in der Allgemeinen Relativitätstheorie.pdf".
• Die Längenkontraktion von Elementarteilchen im Gravitationsfeld wird auch hier angesprochen oder soll dort angesprochen werden: Längenkontraktion im Gravitationsfeld und Längenkontraktion der Materie bei Bewegung
Die nachfolgenden Erklärungen werden aus Sicht eines kosmischen Beobachters beschrieben.
In der folgenden ersten Näherung bleibe ich im Denkschema von Giese:
Ich betrachte nur den Einfluss der Wirkungsquanten eines simplifizierten Strings eines Materie-Elementarteilchens, eines Leptonen-Strings. Dabei lasse ich also die Wirkungsquanten des umgebenden Vakuums außer Acht und gehe auch davon aus, dass sich die Wirkungsquanten der vorbeifliegenden Photonen bereits auf Spiralbahnen bewegen. Die Photonen werden also simplifiziert und quasi wie sich mit Lichtgeschwindigkeit 0c bewegende einzelne Wirkungsquanten behandelt.
|
Virtuelle Wirkungsquanten-Impulse als Störungswellen
Die Störungswirkung der können wir uns nach Giese aus zwei Komponenten bestehend vorstellen:
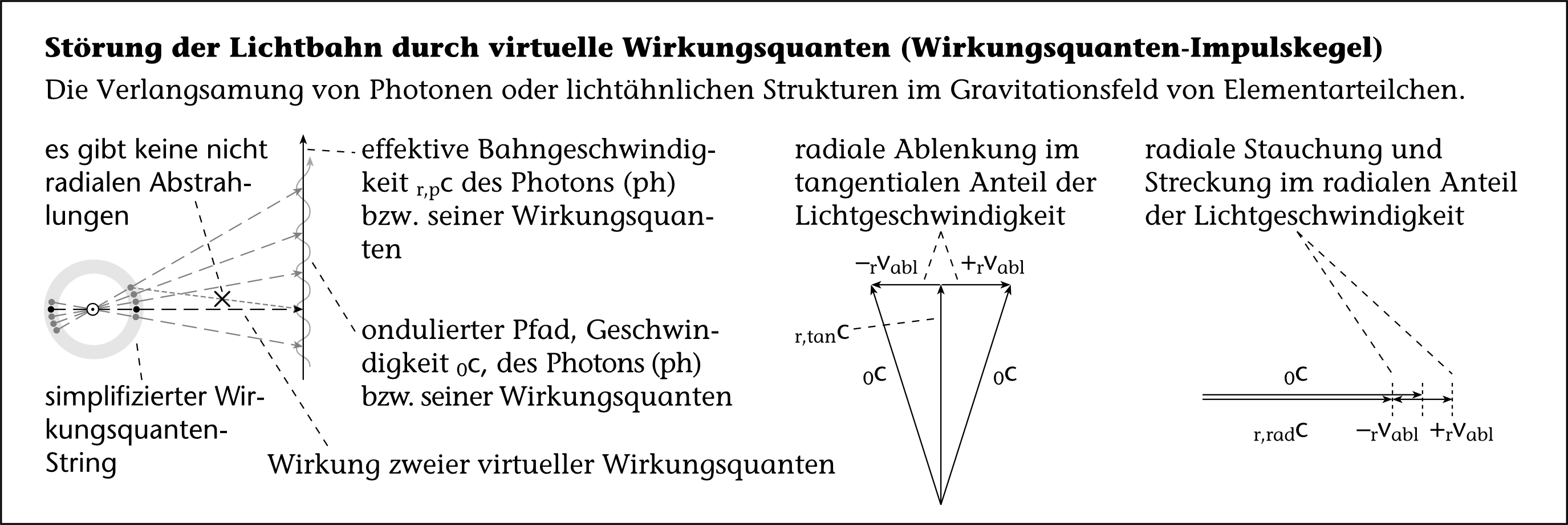
Zunächst wirkt die Störung immer in radialer Richtung, ausgehend von ihrem Entstehungsort auf dem String (siehe , Mitte, und , links). Die Störungswellen sind Longitudinalwellen, breiten sich also ähnlich wie Schallwellen aus. Die Störung hat einen Aspekt, der sich auf die tangentiale Komponente r,tanc, und einen anderen, der sich auf die radiale Komponente r,radc der verlangsamten effektiven Photonen-Geschwindigkeit rc auswirkt (siehe , Mitte und rechts).
Je nach Bewegungsrichtung oder -winkel des Photons relativ zur Verbindungslinie zwischen dem Zentrum des graviradiativ wirkenden Elementarteilchens und des Photons, wird das Photon entsprechend seiner tangentialen und radialen Bewegungsanteile verlangsamt. Dies kommt, weil die virtuellen Wirkungsquanten-Impulse der Graviradiationsquelle das vorbeifliegende Photon in seiner Bewegung stören (siehe , links). Nach dem Basisteilchenmodell von Giese bewegt sich das Photon durch diese Störung auf einem welligen, ondulierten Pfad, wodurch sich seine effektive Bahngeschwindigkeit reduziert.
Wie wir später noch sehen werden, hat dies auch die bekannte der Gravitation zur Folge.
Aus Sicht der Quanten-Fluss-Theorie möchte ich hier kurz eine eingeschobene Bemerkung machen, was in einer detaillierten Betrachtung, ohne Simplifizierung, passiert:
Der durch die Störung welligere, stärker ondulierte Pfad des Lichts, des hier erörterten Bassisteilchenmodells Gieses, stellt sich in der Quanten-Fluss-Theorie bei mehr Detail als engere Wicklung der Helixspiralbahn der Wirkungsquanten des Photons dar (siehe ).
Formalismus
Die von mir nachfolgend benutzte Notation der tiefgestellten Zeichen vor den Variablen drückt den Ort der Beobachtung aus Sicht eines kosmischen Beobachters sowie die Richtung der Lichtbewegung aus. Sie läuft nach dem selben Schema wie im Abschnitt Alterung und strukturierter Raum.
Alle Bewegungen beziehen sich hier auf die unverzerrte Wirkungsquanten-Struktur des Kosmos und nicht auf den verzerrten, strukturierten Raum, des Kosmos, also nicht auf die gekrümmte Raumzeit der Allgemeinen Relativitätstheorie. Der kosmische Beobachter befindet sich in der hier untersuchten Schwarzschild-Metrik also quasi im Unendlichen, wie sich zeigt, wo der Raum unverzerrt, nicht gekrümmt, ist.
Die sich ergebende reduzierte Lichtgeschwindigkeit im dreidimensionalen Raum ist vom Ort und von ihrer Richtung abhängig wie wir sehen werden. In der Quanten-Fluss-Theorie zeigt sich die Raumzeitkrümmung in einer realen Verzerrung des strukturierten Raums in Bezug auf die Wirkunsgquanten-Struktur des Kosmos.
Tangentiale Komponente der Lichtgeschwindigkeit
Die zum Zentrum der Masse radiale Störung der tangentialen Komponente r,tanc der Lichtgeschwindigkeit beim Radius r ergibt sich durch die so ausgelöste zusätzliche radiale Bewegung ±vabl des Photons, die seine tangentiale Geschwindigkeit, aufgrund der eigentlichen Konstanz der Lichtgeschwindigkeit 0c, verringert (siehe , Mitte).
Hierdurch wird das Licht auf einen wellenförmigen, ondulierten Pfad gezwungen, der seinen Weg verlängert und so seine effektive Geschwindigkeit reduziert:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{r,tan}c_{\pm}}\;\;\;=\;\;\;\sqrt{ {{_{\raise -.3ex 0}c}^{2}} - (\pm {_{r}v_{abl}})^{2} } } \] | (QGra.LV.1) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r,tan}c}\;\;\;=\;\;\;\sqrt{ {_{\raise -.3ex 0}c}^{2} - {_{r}v_{abl}^{2}} } } \] | (QGra.LV.2) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r,tan}c}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} \cdot \sqrt{ 1 - \frac{ {_{r}v_{abl}^{2}} }{ {_{\raise -.3ex 0}c}^{2} } } } \] | (QGra.LV.3) | ||
Bei einer zeitlichen Mittelung zwischen den beiden Fällen +vabl und –vabl verändert sich das Ergebnis von r,tanc gegenüber r,tanc± nicht, weil das Vorzeichen von ±vabl durch das Quadrat keine Bedeutung besitzt.
Radiale Komponente der Lichtgeschwindigkeit
Anders ist dies im Fall der radialen Komponente der Lichtgeschwindigkeit r,radc:
Die radiale Störung der radialen Komponente der Lichtgeschwindigkeit ergibt sich aus ihrer longitudinalen Stauchung und Streckung ±vabl (siehe , links). Diese Stauchung und Streckung prägt dem Pfad eine wellenförmige, ondulierte Veränderung des Wegs in seiner Bewegungsrichtung auf:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{r,rad}c_{\pm}}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} \pm {_{r}v_{abl}} } \] | (QGra.LV.4) |
Im zeitlichen Mittel der beiden Fälle +vabl und –vabl bedeutet dies eine Verringerung der radialen Komponente der Lichtgeschwindigkeit r,radc, wie wir gleich sehen werden.
Zur Berechnung des zeitlichen Mittelwerts können wir das Geschehen als Prozess denken: Demnach ist der Fortgang des Prozesses, also seine Alterung r,radaph, im Folgenden kurz als t bezeichnet, dann gleich, wenn das Licht, egal wie schnell es sich auf seinem ondulierten Pfad im Raum bewegt, die gleiche Strecke auf seiner effektiven Bahn zurücklegt; in unserem Fall r,radsph als konstant angenommene Hilfsstrecke, folgend kurz als sph bezeichnet.
Wenn sph also die Strecke ist, die das Licht für den kosmischen Beobachter zurücklegt, und t das ortsabhängige Voranschreiten des Prozesses, dann ergibt sich für r,radc:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{r,rad}c}\;\;\;=\;\;\;\frac{ {s_{ph}} }{ t } } \] | (QGra.LV.5) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}t\;\;\;=\;\;\;\frac{ {s_{ph}} }{ {_{r,rad}c} } } \] | (QGra.LV.6) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}t_{\pm}\;\;\;=\;\;\;\frac{ {s_{ph}} }{ {_{r,rad}c_{\pm}} } } \] | (QGra.LV.7) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}t_{\pm}\;\;\;=\;\;\;\frac{ {s_{ph}} }{ {_{\raise -.3ex 0}c} \pm {_{r}v_{abl}} } } \] | (QGra.LV.8) | ||
Hier ist das Vorzeichen von ±vabl von entscheidender Bedeutung.
Das zeitliche Mittel ist dann:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { t\;\;\;=\;\;\;\frac{ t_{-} + t_{+} }{ 2 } } \] | (QGra.LV.9) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}t\;\;\;=\;\;\;\frac{ 1 }{ 2 } \cdot \left( \frac{ {s_{ph}} }{ {_{\raise -.3ex 0}c} - {_{r}v_{abl}} } + \frac{ {s_{ph}} }{ {_{\raise -.3ex 0}c} + {_{r}v_{abl}} } \right) } \] | (QGra.LV.10) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}t\;\;\;=\;\;\;\frac{ 1 }{ 2 } \cdot \left( \frac{ {s_{ph}} \cdot \left( {_{\raise -.3ex 0}c} + {_{r}v_{abl}} \right) }{ \left( {_{\raise -.3ex 0}c} - {_{r}v_{abl}} \right) \cdot \left( {_{\raise -.3ex 0}c} + {_{r}v_{abl}} \right) } \\ \qquad\qquad\qquad\qquad + \frac{ {s_{ph}} \cdot \left( {_{\raise -.3ex 0}c} - {_{r}v_{abl}} \right) }{ \left( {_{\raise -.3ex 0}c} + {_{r}v_{abl}} \right) \cdot \left( {_{\raise -.3ex 0}c} - {_{r}v_{abl}} \right)} \right) } \] | (QGra.LV.11) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}t\;\;\;=\;\;\;\frac{ 1 }{ 2 } \cdot \left( \frac{ {s_{ph}} \cdot \left( {_{\raise -.3ex 0}c} + {_{r}v_{abl}} \right) }{ {_{\raise -.3ex 0}c^{2}} - {_{r}v_{abl}^{2}} } \\ \qquad\qquad\qquad\qquad + \frac{ {s_{ph}} \cdot \left( {_{\raise -.3ex 0}c} - {_{r}v_{abl}} \right) }{ {_{\raise -.3ex 0}c^{2}} - {_{r}v_{abl}^{2}} } \right) } \] | (QGra.LV.12) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}t\;\;\;=\;\;\;\frac{ {s_{ph}} }{ 2 } \cdot \frac{ \left( {_{\raise -.3ex 0}c} + {_{r}v_{abl}} \right) + \left( {_{\raise -.3ex 0}c} - {_{r}v_{abl}} \right) }{ {_{\raise -.3ex 0}c^{2}} - {_{r}v_{abl}^{2}} } } \] | (QGra.LV.13) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}t\;\;\;=\;\;\;{s_{ph}} \cdot \frac{ {_{\raise -.3ex 0}c} }{ {_{\raise -.3ex 0}c^{2}} - {_{r}v_{abl}^{2}} } } \] | (QGra.LV.14) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}t\;\;\;=\;\;\;\frac{ {s_{ph}} }{ \frac{ {_{\raise -.3ex 0}c^{2}} - {_{r}v_{abl}^{2}} }{ {_{\raise -.3ex 0}c} } } } \] | (QGra.LV.15) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\frac{ {s_{ph}} }{ t }\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}c^{2}} - {_{r}v_{abl}^{2}} }{ {_{\raise -.3ex 0}c} } } \] | (QGra.LV.16) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r,rad}c}\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}c^{2}} - {_{r}v_{abl}^{2}} }{ {_{\raise -.3ex 0}c} } } \] | (QGra.LV.17) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r,rad}c}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} \cdot \left( 1 - \frac{ {_{r}v_{abl}^{2}} }{ {_{\raise -.3ex 0}c^{2}} } \right) } \] | (QGra.LV.18) | ||
Zusammenfassung der tangentialen und radialen Komponente
Wenn wir die Formeln und vergleichen, fällt uns deren Ähnlichkeit auf. Beide Formeln lassen sich zusammenfassen, wenn wir eine Potenz p einführen, die wir für die tangentiale Komponente zu p = ½ und für die radiale zu p = 1 setzen:
Störende Wirkung der virtuellen Wirkungsquanten
(Der effektive Störimpuls) Die effektiv störende Wirkung rpabl des Stroms der eintreffenden virtuellen Wirkungsquanten in den hat, nach Analyse der , die nachfolgend beschriebenen Eigenschaften. Wie wir im unteren Teil der Abbildung sehen, haben die Impulskegel eine Amplitude, die mit der Entfernung abfällt, eine Frequenz und eine Breite:
| • |
Die Ausgangsamplitude soll die Wirkung h eines Wirkungsquants sein. |
| • |
Die Amplitude soll sich beim Abstand r vom String mit 1/r verringern. Diese wurde zuvor schon erklärt. |
| • |
Die Detektor-Frequenz der eintreffenden virtuellen Wirkungsquanten ist offensichtlich die gleiche, wie die Detektor-Frequenz der sie aussendenden Wirkungsquanten auf dem String, also gilt: fele,vwq = fwq . |
| • |
(Die Einwirkungsdauer (Einwirkdauer?) Tkegel der sich drehenden Kegelwand eines Wirkungsquants.) Der Breitenfaktor Tkegel der Impulse hängt davon ab, wie schnell die Impulskegel sich hin- und wegdrehen. Denn rotiert der String doppelt so schnell, dann haben die Impulskegel nur die halbe Zeit auf das vorbeifliegende Licht einzuwirken. Dafür kommen sie doppelt so häufig in der selben Zeit vorbei, was aber schon in der Detektor-Frequenz berücksichtigt ist. Die Drehung der Impulskegel entspricht ihrer Winkelgeschwindigkeit ωele, die bei konstanter Lichtgeschwindigkeit 0c = ωele ⋅ rele der Wirkungsquanten auf dem String bei geringerem Radius rele umgekehrtproportional zunimmt. |
Die effektiv störende Wirkung ist also dem folgenden Produkt proportional:
(Untersuchung – Perspektive Ele-Ebene: Die Wirkungsquanten-Detektorfrequenz fele,vwq sollte nun die Rotationsfrequenz fele sein. Die Einwirkungsdauer (Einwirkdauer?) ist weiterhin nur von der Dauer einer Rotation abhängig, bleibt also Tkegel. Die Amplitude ist nunmehr allerdings nicht einfach nur h, sondern sein Vielfaches proportional zur Energie des Elementarteilchens, entsprechend der Vorstellung, wenn es bei einem Wirkungsquantum mit konstanter Energie h ist, dann muss es bei einem Elementarteilchen ein entsprechendes Vielfaches nele,wq der Energie eines Wirkungsquants sein. XXX XXX XXX XXX XXX XXX)
(———)
(Untersuchung – Perspektive WQ2-Ebene: Hier wird nun unterstellt, dass sich die Wirkungsquanten ein Mal um sich selber drehen, wenn sie eine Wirkungsquanten-Position weiter rotieren. Ist das realistisch möglich? XXX XXX XXX XXX)
(———)
(Untersuchung – fele,vwq = fvwq: Gibt es einen Unterschied zwischen der Abstrahlungsfrequenz der virtuellen Wirkungsquanten und deren innerer Frequenz? XXX XXX XXX)
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { f_{ele,vwq}\;\;\;\overset{?}{=}\;\;\;f_{vwq} } \] | (QGra.LV.Un.fvwq) |
(———)
| ▾ | Analyse der Einheiten: |
Ausdrücke in eckigen Klammern ([Term]) stehen für deren Einheiten oder geben diese explizit an ([Einheiten]).
Die Wirkungsquanten-Frequenz fele,vwq auf dem String können wir aus seiner Rotationsfrequenz fele und der Wirkungsquanten-Anzahl nele,wq des Strings errechnen. Wegen der offensichtlichen Gleichheit der Frequenz des abgestrahlten virtuellen Wirkungsquanten-Stroms und der Wirkungsquanten-Frequenz auf dem String (siehe ) gilt:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { f_{ele,vwq}\;\;\;=\;\;\;f_{wq} } \] | (QGra.LV.28) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { f_{wq}\;\;\;=\;\;\;n_{ele,wq} \cdot f_{ele} } \] | (QGra.LV.29) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}f_{ele,vwq}\;\;\;=\;\;\;n_{ele,wq} \cdot f_{ele} } \] | (QGra.LV.30) | ||
| ▾ | Einschub zur Plausibilität der Quantengravitation: |
Beide Frequenzen, die Wirkungsquanten-Frequenz auf dem String und die abgestrahlte virtuelle Wirkungsquanten-Frequenz, sind grundsätzlich unabhängig von der Veränderung ihrer Ausbreitungsgeschwindigkeit.
Dies ist eine sehr wichtige Eigenschaft der hier entwickelten Quantengravitation.
Die Wirkungsquanten-Frequenzen sind unabhängig von der Veränderung ihrer Ausbreitungsgeschwindigkeit
Wenn die beiden Frequenzen fele,vwq und fwq die gleichen sind, dann ist die Veränderung der Dichte rρvwq der virtuellen Wirkungsquanten-Impulse ausschließlich von der Veränderung der Ausbreitungsgeschwindigkeit der Impulse abhängig. Genauso ist die Veränderung der Wirkungsquanten-Dichte releρele,wq auf dem String ausschließlich durch die Veränderung der Geschwindigkeit von dessen Rotation bestimmt.
Beide Geschwindigkeiten variieren von Ort zu Ort also mit der Verlangsamung der Ausbreitung des Lichts im Raum r,pc, die wir hier ja insgesamt berechnen wollen, mit dem Abstand r und ihrer Bewegungsrichtung p.
Die Variation beider Dichten mit der Ausbreitungsgeschwindigkeit ihrer (virtuellen) Wirkungsquanten entspricht der der Detektorwellenlänge xλwq,d von Licht bei sich ändernder Lichtgeschwindigkeit aus Formel . Hieraus können wir die Dichte bei einer bestimmten Ausbreitungsgeschwindigkeit ableiten:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}\lambda_{wq,d}}\;\;\;=\;\;\;{_{\raise -.3ex 0}\lambda_{wq,d}} \cdot {_{x}\alpha} } \] | (ZAF.RED.1) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}\rho_{wq}}\;\;\;=\;\;\;\frac{ 1 }{ {_{x}\lambda_{wq,d}} } } \] | (QGra.LV.31) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}\rho_{wq}}\;\;\;=\;\;\;\frac{ 1 }{ {_{\raise -.3ex 0}\lambda_{wq,d}} \cdot {_{x}\alpha} } } \] | (QGra.LV.32) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}\rho_{wq}}\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}\rho_{wq}} }{ {_{x}\alpha} } } \] | (QGra.LV.33) |
Und wir können sehen, dass die Veränderung der Ausbreitungsgeschwindigkeit der Veränderung der Dichte genau so entgegen wirkt, dass die Frequenz gleich bleibt, egal an welchem Ort oder in welcher Richtung die Bewegung stattfindet:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}c}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} \cdot {_{x}\alpha} } \] | (ZAF.Alt.14) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{x}f_{wq}}\;\;\;=\;\;\;{_{x}\rho_{wq}} \cdot {_{x}c} } \] | (QGra.LV.34) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}f_{wq}}\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}\rho_{wq}} }{ {_{x}\alpha} } \cdot {_{\raise -.3ex 0}c} \cdot {_{x}\alpha} } \] | (QGra.LV.35) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{x}f_{wq}}\;\;\;=\;\;\;{_{\raise -.3ex 0}\rho_{wq}} \cdot {_{\raise -.3ex 0}c} } \] | (QGra.LV.36) |
Die Frequenz der Wirkungsquanten ist also tatsächlich unabhängig von der Ausbreitungsgeschwindigkeit der Wirkungsquanten am Ort der beobachtet wird.
Dies ist eine wichtige Erkenntnis:
Durch die Unabhängigkeit der virtuellen Wirkungsquanten-Frequenz von der Veränderung ihrer Ausbreitungsgeschwindigkeit und der nachfolgend gezeigten Berechnung der Gravitation über die statistische Standardabweichung, lässt sich die Quantengravitation vieler Teilchen, also größerer Massen, beliebig kombinieren.
Der Schluss unterstreicht, dass wir es hier mit einer plausiblen Struktur der Quantengravitation zu tun haben.
In die Formel der effektiv störenden Wirkung eingesetzt erhalten wir:
(Untersuchung – Perspektive Ele-Ebene: Wir sehen also, dass diese Perspektive schlussendlich genau in die gleiche Formel mündet. XXX XXX XXX XXX XXX XXX XXX XXX)
(———)
Es ist nun wünschenswert den Breitenfaktor Tkegel am Ende so zu formulieren, dass die uns generell noch unbekannte Wirkungsquanten-Anzahl nele,wq sich weg kürzt.
Für den Breitenfaktor gilt nach den obigen Eigenschaften:
Wir können nun die Winkelgeschwindigkeit ωele so umformulieren, dass sie durch die Wirkungsquanten-Anzahl nele,wq ausgedrückt wird. Dazu schauen wir nach ihrer Beziehung zur Energie des Elementarteilchen-Strings und drücken diese schließlich durch seine Masse aus:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { E_{ele}\;\;\;=\;\;\;h \cdot f_{ele} } \] | (Un.10) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \omega_{ele}\;\;\;=\;\;\;2 \pi \cdot f_{ele} } \] | (QGra.LV.40) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}E_{ele}\;\;\;=\;\;\;h \cdot \frac{ \omega_{ele} }{ 2 \pi } } \] | (QGra.LV.41) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}E_{ele}\;\;\;=\;\;\;\hbar \cdot \omega_{ele} } \] | (QGra.LV.42) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}\omega_{ele}\;\;\;=\;\;\;\frac{ E_{ele} }{ \hbar } } \] | (QGra.LV.43) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { E_{ele}\;\;\;=\;\;\;m_{ele} \cdot {_{\raise -.3ex 0}c^{2}} } \] | (FP.3) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}T_{kegel}\;\;\;=\;\;\;g_{\omega} \cdot \frac{ \hbar }{ E_{ele} } } \] | (QGra.LV.44) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}T_{kegel}\;\;\;=\;\;\;g_{\omega} \cdot \frac{ \hbar }{ m_{ele} \cdot {_{\raise -.3ex 0}c^{2}} } } \] | (QGra.LV.45) | ||
| ▾ | Analyse der Einheiten: |
Ausdrücke in eckigen Klammern ([Term]) stehen für deren Einheiten oder geben diese explizit an ([Einheiten]).
Weil jedes Wirkungsquant eine konstante Masseeinheit mwq ist, kann die Masse mele eines Strings über seine Wirkungsquanten-Anzahl nele,wq folgendermaßen beschrieben werden:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { m_{ele}\;\;\;=\;\;\;n_{ele,wq} \cdot m_{wq} } \] | (FP.2) |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}T_{kegel}\;\;\;=\;\;\;g_{\omega} \cdot \frac{ \hbar }{ n_{ele,wq} \cdot m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} } } \] | (QGra.LV.53) |
Setzen wir diese Werte nun in die Formel der effektiv störenden Wirkung ein, ergibt sich:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r}p_{abl}}\;\;\;=\;\;\;g_{h} \cdot \frac{ h \cdot g_{\omega} \cdot \frac{ \hbar }{ n_{ele,wq} \cdot m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} } \cdot n_{ele} \cdot f_{ele} }{ r } } \] | (QGra.LV.54) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r}p_{abl}}\;\;\;=\;\;\;g_{\omega} \cdot g_{h} \cdot \frac{ \hbar }{ m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} } \cdot \frac{ h \cdot n_{ele,wq} \cdot f_{ele} }{ n_{ele,wq} \cdot r } } \] | (QGra.LV.55) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r}p_{abl}}\;\;\;=\;\;\;g_{\omega} \cdot g_{h} \cdot \frac{ \hbar }{ m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} } \cdot \frac{ h \cdot f_{ele} }{ r } } \] | (QGra.LV.56) | ||
Über Plancks Proportionalität von Energie und Frequenz aus Formel und Einstens Energie-Masse-Äquivalenz aus Formel können wir die effektiv störende Wirkung durch die Masse mele ausdrücken. So formuliert benötigen wir diese im weiteren Verlauf:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r}p_{abl}}\;\;\;=\;\;\;g_{\omega} \cdot g_{h} \cdot \frac{ \hbar }{ m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} } \cdot \frac{ E_{ele} }{ r } } \] | (QGra.LV.57) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r}p_{abl}}\;\;\;=\;\;\;g_{\omega} \cdot g_{h} \cdot \frac{ \hbar }{ m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} } \cdot \frac{ m_{ele} \cdot {_{\raise -.3ex 0}c^{2}} }{ r } } \] | (QGra.LV.58) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r}p_{abl}}\;\;\;=\;\;\;g_{\omega} \cdot g_{h} \cdot \frac{ \hbar }{ m_{wq} } \cdot \frac{ m_{ele} }{ r } } \] | (QGra.LV.59) | ||
Die effektiv störende Wirkung ist demnach proportional zur Masse des Strings und umgekehrtproportional zum Abstand zu ihm.
Näherung bei großen Abständen
… im Verhältnis zum Radius des gravitativ wirkenden Elementarteilchens
Wie in dargestellt, entstehen die virtuellen Wirkungsquanten aus den Wirkungsquanten des Strings. Die abgestrahlten virtuellen Wirkungsquanten-Impulse nehmen, wie schon gesagt, mit dem Abstand r vom String ab. In der weiteren Herleitung sollen ausschließlich im Verhältnis zum Radius des Elementarteilchens rele große Abstände r eine Rolle spielen.
In diesem Fall wird der Elementarteilchen-Radius rele auf derartig große Distanzen irrelevant und nur der Abstand von deren Zentrum betrachtet, vorübergehend rc genannt; anschließend dann wieder r, der Einfachheit halber:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { r_{ele}\;\;\;\ll\;\;\;r } \] | (QGra.LV.60) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { r_{c}\;\;\;=\;\;\; r \pm r_{ele} } \] | (QGra.LV.61) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}r_{c}\;\;\;\approx\;\;\;r } \] | (QGra.LV.62) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { r_{c}\;\;\;\mapsto\;\;\; r } \] | (QGra.LV.63) | ||
Im Folgenden wird in Aufklapptexten die Rechnung auch ohne diese Näherung, für kleine Distanzen im Nahbereich vom Elementarteilchen, ausgeführt.
Zwei Stellen des Wirkungsquanten-Strings wirken gleichzeitig
Es wirken nun immer genau zwei Stellen auf einem Elementarteilchen-String zugleich (siehe , Mitte, und ), weil die virtuellen Wirkungsquanten nur genau radial, senkrecht zur Bewegungsrichtung der Wirkungsquanten auf dem String, abgestrahlt werden.
(Untersuchung – Perspektive Ele-Ebene: Hier ist in der neuen Perspektive zu berücksichtigen, dass es sich bei der Abstrahlung eines Photons bei näherer Betrachtung um einen Doppelwandigen Impulskegel handelt. Die Wirkung h des Impulskegels eines Wirkungsquants enthält die Doppelwandigkeit bereits. Im Falle von Leptonen kommt durch das Auf- und wieder Einfalten seiner schwingenden Struktur ebenfalls von jeder der beiden Seiten des Stings ein eigener Impuls. XXX XXX XXX XXX XXX)
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r}p_{ele,abl}}\;\;\;=\;\;\;2 \cdot {_{r}p_{abl}} } \] | (QGra.LV.64) |
| ▾ | Rechnung für Nahbereich: |
Ohne , also bei einigen Vielfachen des Elementarteilchen-Radius, ergibt sich folgende Rechnung. Es bleibt die Simplifizierung des Leptonen-Strings und Vakuums:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r\pm}p_{ele,abl}}\;\;\;=\;\;\;{_{r+r_{ele}}p_{abl}} + {_{r-r_{ele}}p_{abl}} } \] | (QGra.LV.65) |
Gravitative Wirkung eines einzelnen Elementarteilchens auf Licht
Die sich durch ein einzelnes Elementarteilchen aus der Störung rpele,abl ergebende Geschwindigkeit der Ablenkung rvele,abl ist dann proportional zu dieser Störung und berechnet sich durch Einsetzen zu:
| ▾ | Analyse der Einheiten: |
Ausdrücke in eckigen Klammern ([Term]) stehen für deren Einheiten oder geben diese explizit an ([Einheiten]).
| ▾ | Rechnung für Nahbereich: |
Ohne , also bei einigen Vielfachen des Elementarteilchen-Radius, ergibt sich folgende Rechnung. Es bleibt die Simplifizierung des Leptonen-Strings und Vakuums:
Diese Ablenkungsgeschwindigkeit eingesetzt in Formel ergibt:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r,p}c_{ele}}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} \cdot \left( 1 - \frac{ \left( g_{v} \cdot 2 \cdot g_{\omega} \cdot \frac{ g_{h} \cdot \frac{ \hbar }{ m_{wq} } \cdot m_{ele} }{ r } \right)^{2} }{ {_{\raise -.3ex 0}c^{2}} } \right)^{p} } \] | (QGra.LV.80) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r,p}c_{ele}}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} \cdot \left( 1 - 4 \cdot \frac{ \left( g_{v} \cdot g_{\omega} \cdot g_{h} \cdot \frac{ \hbar }{ m_{wq} } \right)^{2} \cdot m_{ele}^{2} }{ {_{\raise -.3ex 0}c^{2}} \cdot r^{2} } \right)^{p} } \] | (QGra.LV.81) | ||
| ▾ | Analyse der Einheiten: |
Ausdrücke in eckigen Klammern ([Term]) stehen für deren Einheiten oder geben diese explizit an ([Einheiten]).
| ▾ | Rechnung für Nahbereich: |
Ohne , also bei einigen Vielfachen des Elementarteilchen-Radius, ergibt sich folgende Rechnung. Es bleibt die Simplifizierung des Leptonen-Strings und Vakuums:
Setzen wir hier die Gravitationskonstante so ein, wie sie sich in der nachfolgenden Herleitung für große Massen in Formel zeigt, dann bekommen wir für ein einzelnes Elementarteilchen:
| ▾ | Analyse der Einheiten: |
Ausdrücke in eckigen Klammern ([Term]) stehen für deren Einheiten oder geben diese explizit an ([Einheiten]).
| ▾ | Rechnung für Nahbereich: |
Ohne , also bei einigen Vielfachen des Elementarteilchen-Radius, ergibt sich folgende Rechnung. Es bleibt die Simplifizierung des Leptonen-Strings und Vakuums:
Wie wir gleich sehen werden ergibt sich für die Gravitation einer großen Masse durch einen statistischen Effekt eine andere Formel für die Lichtverlangsamung durch Graviradiation oder Gravitation.
Gravitative Wirkung einer zentralen Masse auf Licht
Die Zufallsstatistik kommt ins Spiel
Im Fall einer zentralen Masse entsteht die insgesamt resultierende Störungsgeschwindigkeit rvabl aus der Summe aller einzelnen Störungen durch die virtuellen Wirkungsquanten. Allerdings erreichen die einzelnen Störungen in diesem Fall die Bahn des Photons in zufälligen Zeitabständen.
Zufällig deshalb, weil letztendlich nicht nur die Wirkungsquanten des einen Elementarteilchen-Strings mele wirken, sondern auch die aller weiteren Elementarteilchen einer zentralen Masse M. Aus diesem Grund müssen die Regeln der Zufallsstatistik in Form der Standardabweichung Anwendung finden. Das bedeutet, dass sich die effektive Ablenkungsgeschwindigkeit zur Quadratwurzel der Summe der einzelnen Störungen berechnet. Wir haben gv oben schon als Proportionalitätskonstante eingeführt.
Zuerst führt Formel zur Definition der nicht statistischen effektiven Wirkung rpmas,abl der Zentralmasse. Bei der Berechnung der Standardabweichung bezieht sich das Ziehen der Quadratwurzel ausschließlich auf den Wert der Ablenkungsgeschwindigkeit ohne Standardabweichung und nicht auf seine Einheiten. Daher ist der Wert getrennt von seinen Einheiten zu berechnen. Diese etwas umständliche Art der Darstellung ersetze ich durch die Einführung der Konstanten gs, die ausschließlich zur Beibehaltung der ursprünglichen Einheiten genutzt wird und damit keinen Trick zur Verschleierung verkehrter Einheiten darstellt:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { m_{ele}\;\;\;\mapsto\;\;\;M } \] | (QGra.LV.95) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r}p_{mas,abl}}\;\;\;=\;\;\;2 \cdot g_{\omega} \cdot \frac{ g_{h} \cdot \frac{ \hbar }{ m_{wq} } \cdot M }{ r } } \] | (QGra.LV.96) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} \require{cancel} { {_{r}v_{mas,abl,\cancel{standabw}}}\;\;\;\sim\;\;\;{_{r}p_{mas,abl}} } \] | (QGra.LV.97) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} \require{cancel} { \Rightarrow\hspace{10mm}{_{r}v_{mas,abl,\cancel{standabw}}}\;\;\;=\;\;\;g_{v} \cdot {_{r}p_{mas,abl}} } \] | (QGra.LV.98) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} \require{cancel} { {_{r}v_{mas,abl}}\;\;\;=\;\;\;\sqrt{ wert\left({_{r}v_{mas,abl,\cancel{standabw}}}\right) } \cdot \left[ \frac{ m }{ s } \right] } \] | (QGra.LV.99) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { g_{s}\;\;\;≔\;\;\;1 \cdot \frac{ m }{ s } } \] | (QGra.LV.100) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} \require{cancel} { \Rightarrow\hspace{10mm}{_{r}v_{mas,abl}}\;\;\;=\;\;\;\sqrt{ g_{s} \cdot {_{r}v_{mas,abl,\cancel{standabw}}} } } \] | (QGra.LV.101) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r}v_{mas,abl}}\;\;\;=\;\;\;\sqrt{ g_{s} \cdot g_{v} \cdot {_{r}p_{mas,abl}} } } \] | (QGra.LV.102) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r}v_{mas,abl}}\;\;\;=\;\;\;\sqrt{ g_{s} \cdot g_{v} \cdot 2 \cdot g_{\omega} \cdot \frac{ g_{h} \cdot \frac{ \hbar }{ m_{wq} } \cdot M }{ r } } } \] | (QGra.LV.103) | ||
| ▾ | Analyse der Einheiten: |
Ausdrücke in eckigen Klammern ([Term]) stehen für deren Einheiten oder geben diese explizit an ([Einheiten]).
Die Standardabweichung, ihre Quadratwurzel, wird nur auf die Werte aber nicht auf die Einheiten angewendet. Um mathematisch äquivalentes in einfacher und gut lesbarer Form zu erreichen, wird hier die Konstante gs in der Berechnung der Standardabweichung eingeführt.
Der statistische Effekt der Störung ist eine entscheidende Einsicht Gieses, um die Entstehung der Lichtverlangsamung und -beugung im Gravitationsfeld und damit die Gravitation zu verstehen.
Lichtgeschwindigkeitsänderung im Gravitationsfeld
Gravitation durch die Wirkung der Elementarteilchen-Strukturen einer Masse
Wenn nun die Formel in die Formel eingesetzt wird, ergibt sich:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r,p}c_{mas}}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} \cdot \left( 1 - \frac{ \left( \sqrt{ g_{s} \cdot g_{v} \cdot 2 \cdot g_{\omega} \cdot \frac{ g_{h} \cdot \frac{ \hbar }{ m_{wq} } \cdot M }{ r } } \right)^{2} }{ {_{\raise -.3ex 0}c}^{2} } \right)^{p} } \] | (QGra.LV.104) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}{_{r,p}c_{mas}}\;\;\;=\;\;\;{_{\raise -.3ex 0}c} \cdot \left( 1 - 2 \cdot \frac{ g_{s} \cdot g_{v} \cdot g_{\omega} \cdot g_{h} \cdot \frac{ \hbar }{ m_{wq} } \cdot M }{ {_{\raise -.3ex 0}c}^{2} \cdot r } \right)^{p} } \] | (QGra.LV.105) | ||
Vergleichen wir unser Ergebnis mit der nachfolgenden Formel für die Änderung der Lichtgeschwindigkeit im Gravitationsfeld der Allgemeinen Relativitätstheorie in der äußeren Lösung der Schwarzschild-Metrik, die eine einzelne zentrale Masse beschreibt, so ergibt sich für die Gravitationskonstante G:
| ▾ | Analyse der Einheiten: |
Ausdrücke in eckigen Klammern ([Term]) stehen für deren Einheiten oder geben diese explizit an ([Einheiten]).
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { G\;\;\;=\;\;\;6,67384 \cdot 10^{-11} \cdot \frac{ m^3 }{ \mathit{kg} \cdot s^2 } } \] | (QGra.LV.108) |
Die Einheiten der Gravitationskonstanten passen tatsächlich genau zum hergeleiteten Wert:
Die Formel entspricht der in Experimenten beobachteten Shapiro-Verzögerung des Lichts im Gravitationsfeld. Eine nähere Analyse der findet sich im nächsten Abschnitt.
Was haben wir nun im Vergleich zu Gieses Basisteilchenmodell gewonnen?
Es gibt einen wesentlichen Unterschied zu Gieses Basisteilchenmodell:
Der Fortschritt im Vergleich zu Gieses Formulierung der Lichtverlangsamung besteht darin, dass sich so ein nachvollziehbarer Zusammenhang mit der Masse des anziehenden, kugelförmigen Objekts ergibt und nicht „nur“ mit der Anzahl an Elementarteilchen in diesem Objekt.
Es gibt noch mehr Unterschiede im Vergleich der Quanten-Fluss-Theorie mit dem Basisteilchenmodell.
Vereinheitlichung der Physik
Die Quanten-Fluss-Theorie ist in der Lage, eine wichtige Eigenschaft des Gravitationsfelds entsprechend der Allgemeinen Relativitätstheorie aus der hier beschriebenen Struktur der Elementarteilchen und Grundformeln der Quantenphysik herzuleiten:
Mit einer Simplifizierung des Leptonen-Strings erhalten wir im Rahmen der Quanten-Fluss-Theorie die korrekte Veränderung der Lichtgeschwindigkeit im Gravitationsfeld einer homogenen Massenkugel. Dies kann als deutlicher Hinweis auf eine Vereinheitlichung von Quantenphysik und Allgemeiner Relativitätstheorie gewertet werden.
Der , die und die wird in den folgenden Abschnitten erklärt.
| → |
|
| |
Struktur der Gravitationskonstanten |
|
| ← |
|
Über die Formel bekommen wir eine Idee der Struktur der Gravitationskonstanten, wobei die Werte von vier der sechs Konstanten noch nicht bekannt sind.
Der Wert der Gravitationskonstanten kann leider noch nicht hergeleitet werden, aber wir sind hiermit diesem Ziel einen Schritt näher gekommen. Und zwar dadurch, mehr Einblick in die Strukturen zu gewinnen, die Grundlage ihrer Entstehung sind.
In der Allgemeinen Relativitätstheorie existiert keinerlei Ansatz zum Verständnis der Gravitationskonstanten. Sie wird dort, und auch in jeder anderen mir bekannten Theorie, schlicht als gemessener Wert eingesetzt.
Es besteht also Hoffnung, das hohe Ziel ihrer Herleitung mit der Quanten-Fluss-Theorie in Zukunft zu erreichen.
Analyse der strukturellen Abhängigkeiten der Gravitationskonstanten
Schauen wir uns die Formeln zur Herleitung der an, dann finden wir die sich am Schluss ergebende Gravitationskonstante aus Formel im Grunde bereits in Formel :
Die zentrale Rolle der Gravitationskonstanten G besteht offenbar darin, die Proportionalität des Produkts der Ablenkungsgeschwindigkeit rvele,abl mit dem Abstand r zur Masse mele eines Elementarteilchens auszudrücken:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}2 \cdot \frac{ G }{ g_{s} }\;\;\;=\;\;\;\frac{ {_{r}v_{ele,abl}} \cdot r }{ m_{ele} } } \] | (QGra.SG.3) |
| ▾ | Proportionalität: |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r}v_{ele,abl}}\;\;\;\sim\;\;\;\frac{ m_{ele} }{ r } } \] | (QGra.SG.4) |
Bei, für gewöhnlich, konstanter Masse mele ergibt sich die vereinfachte Proportionalität:
Weil sowohl die Ablenkungsgeschwindigkeit rvele,abl als auch die Masse mele proportional zur Anzahl nele,wq der Wirkungsquanten im Elementarteilchen sind (siehe Formeln und ), ergibt sich, herunter gebrochen auf ein einzelnes Wirkungsquant, wenn wir berücksichtigen, dass dann nicht mehr beide gegenüberliegenden Seiten des Elementarteilchen-Strings gleichzeitig wirken können (siehe Formeln und ):
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { m_{ele}\;\;\;=\;\;\;n_{ele,wq} \cdot m_{wq} } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{r}p_{ele,abl}}\;\;\;=\;\;\;2 \cdot {_{r}p_{abl}} } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{r}v_{ele,abl}}\;\;\;=\;\;\;g_{v} \cdot {_{r}p_{ele,abl}} } \] | () | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}\frac{ G }{ g_{s} }\;\;\;=\;\;\;\frac{ {_{r}v_{wq,abl}} \cdot r }{ m_{wq} } } \] | (QGra.SG.7) | ||
| ▾ | Proportionalität: |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r}v_{wq,abl}}\;\;\;\sim\;\;\;\frac{ 1 }{ r } } \] | (QGra.SG.8) |
XXX XXX XXX XXX XXX XXX XXX XXX XXX XXX XXX
Irrelevanz der Einwirkdauer und des Wirkimpulses
Bemerkenswert ist dabei, dass die Einwirkdauer Tkegel der Impulskegelwand und des sich aus ihr ergebenden Wirkimpulses rpele,abl keine Rolle für den Wert der Gravitationskonstanten spielen. Dies kommt, weil sie sich gegenseitig wegkürzen, wenn wir die Gravitationskonstante aus ihren Einzelkonstanten berechnen.
Die Konstante gh berechnet sich aus Formel zu:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{r}p_{abl}}\;\;\;=\;\;\;g_{h} \cdot \frac{ h \cdot T_{kegel} \cdot n_{ele,wq} \cdot f_{ele} }{ r } } \] | () | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}g_{h}\;\;\;=\;\;\;\frac{ {_{r}p_{abl}} \cdot r }{ h \cdot T_{kegel} \cdot n_{ele,wq} \cdot f_{ele} } } \] | (QGra.SG.9) | ||
| ▾ | Proportionalität: |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r}p_{abl}}\;\;\;\sim\;\;\;\frac{ T_{kegel} \cdot n_{ele,wq} \cdot f_{ele} }{ r } } \] | (QGra.SG.10) |
Bei, für gewöhnlich, konstanter Masse mele, und damit Tkegel, nele,wq und fele, ergibt sich die vereinfachte Proportionalität:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r}p_{abl}}\;\;\;\sim\;\;\;\frac{ 1 }{ r } } \] | (QGra.SG.11) |
Die Konstante gω berechnet sich aus Formel zu:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { T_{kegel}\;\;\;=\;\;\;g_{\omega} \cdot \frac{ \hbar }{ n_{ele,wq} \cdot m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} } } \] | () | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}g_{\omega}\;\;\;=\;\;\;\frac{ T_{kegel} \cdot n_{ele,wq} \cdot m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} }{ \hbar } } \] | (QGra.SG.12) | ||
| ▾ | Konstanz: |
So wird ersichtlich, dass sich eine neue Konstante ergibt, die ħ sowie gω verbindet und die ich ħω nenne:
Die Konstante gv berechnet sich aus den Formeln und zu:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{r}p_{ele,abl}}\;\;\;=\;\;\;2 \cdot {_{r}p_{abl}} } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { {_{r}v_{ele,abl}}\;\;\;=\;\;\;g_{v} \cdot {_{r}p_{ele,abl}} } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r}v_{ele,abl}}\;\;\;=\;\;\;g_{v} \cdot 2 \cdot {_{r}p_{abl}} } \] | (QGra.SG.19) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}g_{v}\;\;\;=\;\;\;\frac{ {_{r}v_{ele,abl}} }{ 2 \cdot {_{r}p_{abl}} } } \] | (QGra.SG.20) | ||
| ▾ | Proportionalität: |
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}{_{r}v_{ele,abl}}\;\;\;\sim\;\;\;{_{r}p_{abl}} } \] | (QGra.SG.21) |
Nach dem Einsetzen dieser drei Konstanten in Formel kann dann tatsächlich erheblich gekürzt werden:
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { G\;\;\;=\;\;\;g_{s} \cdot g_{v} \cdot g_{\omega} \cdot g_{h} \cdot \frac{ \hbar }{ m_{wq} } } \] | () | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}G\;\;\;=\;\;\;g_{s} \cdot \frac{ {_{r}v_{ele,abl}} }{ 2 \cdot {_{r}p_{abl}} } \cdot \frac{ T_{kegel} \cdot n_{ele,wq} \cdot m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} }{ \hbar } \\ \qquad\qquad\qquad \cdot \frac{ {_{r}p_{abl}} \cdot r }{ h \cdot T_{kegel} \cdot n_{ele,wq} \cdot f_{ele} } \cdot \frac{ \hbar }{ m_{wq} } } \] | (QGra.SG.22) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}G\;\;\;=\;\;\;g_{s} \cdot \frac{ {_{r}v_{ele,abl}} }{ 2 \cdot {_{r}p_{abl}} } \cdot \frac{ n_{ele,wq} \cdot m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} }{ \hbar } \\ \qquad\qquad\qquad \cdot \frac{ {_{r}p_{abl}} \cdot r }{ h \cdot n_{ele,wq} \cdot f_{ele} } \cdot \frac{ \hbar }{ m_{wq} } } \] | (QGra.SG.23) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}G\;\;\;=\;\;\;g_{s} \cdot \frac{ {_{r}v_{ele,abl}} }{ 2 } \cdot \frac{ n_{ele,wq} \cdot m_{wq} \cdot {_{\raise -.3ex 0}c^{2}} }{ \hbar } \\ \qquad\qquad\qquad \cdot \frac{ r }{ h \cdot n_{ele,wq} \cdot f_{ele} } \cdot \frac{ \hbar }{ m_{wq} } } \] | (QGra.SG.24) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}G\;\;\;=\;\;\;g_{s} \cdot \frac{ {_{r}v_{ele,abl}} }{ 2 } \cdot n_{ele,wq} \cdot {_{\raise -.3ex 0}c^{2}} \\ \qquad\qquad\qquad \cdot \frac{ r }{ h \cdot n_{ele,wq} \cdot f_{ele} } } \] | (QGra.SG.25) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}G\;\;\;=\;\;\;g_{s} \cdot \frac{ {_{r}v_{ele,abl}} }{ 2 } \cdot {_{\raise -.3ex 0}c^{2}} \cdot \frac{ r }{ h \cdot f_{ele} } } \] | (QGra.SG.26) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}G\;\;\;=\;\;\;g_{s} \cdot \frac{ {_{r}v_{ele,abl}} \cdot r }{ 2 } \cdot \frac{ {_{\raise -.3ex 0}c^{2}} }{ h \cdot f_{ele} } } \] | (QGra.SG.27) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}G\;\;\;=\;\;\;g_{s} \cdot \frac{ {_{r}v_{ele,abl}} \cdot r }{ 2 } \cdot \frac{ 1 }{ m_{ele} } } \] | (QGra.SG.28) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}G\;\;\;=\;\;\;g_{s} \cdot \frac{ 1 }{ 2 } \cdot \frac{ {_{r}v_{ele,abl}} \cdot r }{ m_{ele} } } \] | () | ||
Es ergibt sich die Formel , wie zu erwarten.
Interessanterweise haben ausschließlich die Ablenkgeschwindigkeit rvele,abl, der Abstand r vom Massenzentrum und die Masse mele des Elementarteilchens einen Einfluss auf den Wert der Gravitationskonstanten. Die Einwirkdauer Tkegel der Impulskegelwand, der Wirkimpuls rpele,abl und die anderen Variablen und Konstanten fallen durchs Kürzen alle weg. XXX XXX XXX
XXX XXX XXX XXX XXX XXX XXX
XXX
XXX XXX XXX XXX XXX XXX XXX
XXX
XXX XXX XXX XXX XXX XXX XXX
| → |
|
| |
Längenkontraktion |
|
Die Shapiro-Verzögerung zusammen mit einer gravitativen Längenkontraktion erzeugt die Raumzeitkrümmung
| ← |
|
Erst eine Längenkontraktion der angenommenen Elementarteilchen-Struktur im Gravitationsfeld macht im Hinblick auf ihre strukturellen Schwingungen Sinn.
Die Art der Längenkontraktion im Gravitationsfeld der Quanten-Fluss-Theorie ergibt sich dazu plausibel aus Gieses Herleitung dieser gravitativen Längenkontraktion. Der von ihm angeführte Mechanismus ist im Grunde der gleiche, wie der der Längen- oder Lorentzkontraktion von im Raum bewegter Materie und entspricht so der Entstehung eines Heaviside-Ellipsoiden.
Demnach ist für die Entstehung eines Heaviside-Ellipsoiden die anisotrope Ausbreitung der seine Struktur bestimmenden Wechselwirkungsteilchen ausschlaggebend. Genauer gesagt ist es ihre in einer Raumrichtung abweichende Geschwindigkeit im Verhältnis zu den Geschwindigkeiten der anderen beiden Raumrichtungen, relativ zum Schwerpunkt des Elementarteilchens.
Längenkontraktion von Elementarteilchen im Gravitationsfeld der Quantengravitation
Die strukturelle Geometrie von Elementarteilchen verändert sich nach Giese in ihrer Ausdehnung in einem Gravitationsfeld in tangentialer und radialer Richtung zur Zentralmasse, wenn w0 ihre Ausdehnung ohne diese Verzerrung ist. Adaptiert auf Formel ergibt sich:
Wobei wir, wie oben schon erläutert, für die tangentiale Komponente relativ zur Zentralmasse p = ½ und für die radiale Komponente p = 1 setzen. So, dass die tangentiale Komponente, wegen des Exponenten exp mit exp = p – ½ = 0, unverändert bleibt und nur die radiale Komponente, wegen des Exponenten exp mit exp = p – ½ = ½, eine Veränderung erfährt.
Diese geometrische Verzerrung der Struktur von Elementarteilchen im Gravitationsfeld ergibt sich nach Giese, weil sich mit der Veränderung der Lichtgeschwindigkeit auch die Ausbreitungsgeschwindigkeit der Wechselwirkungsteilchen ändert, die die Wirkungsquanten im String aneinander binden. Dieser der Lorentzkontraktion äquivalente Effekt im Zusammenhang mit Bindungsfeldern ist, wie schon gesagt, auch als Heaviside-Ellipsoid bekannt.
Elementarteilchen-Spin-Frequenz gebietet die Längenkontraktion
| ▾ | Notizen |
• Diese Herleitung findet sich nun extrem ähnlich in Elementarteilchen im Gravitationsfeld, also dort anpassen.
Die innere Logik der Elementarteilchen-Struktur gebietet bei anisotroper, je Richtung unterschiedlicher Lichtgeschwindigkeit eine entsprechende anisotrope Verzerrung seiner Struktur. Denn die Möglichkeit der Spin-Rotation der Elementarteilchen-Struktur – im Sinne der Lichtuhr Einstens, also des äußeren Haupt-Spins des Elementarteilchens – in jeder Raumrichtung bedingt, dass die lichtähnlichen Teilstrukturen des Elementarteilchen-Modells in Bezug auf jede Rotation in jeder denkbaren Raumrichtung mit der gleichen Frequenz rotieren (siehe ).
Um zu zeigen, dass sich die anisotrope Lichtgeschwindigkeit und die anisotrope Strukturverzerrung bezüglich der Rotationsfrequenz des Spins aufheben, möchte ich die reine Bewegung und deren Frequenz entlang der beiden Halbachsen des Heaviside-Ellipsoiden eines Elementarteilchens betrachten. Die Bewegung auf ihrem Weg r,pwmas mit der Geschwindigkeit r,pcmas:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { _{r,p}c_{mas}\;\;\;=\;\;\;\frac{ _{r,p}w_{mas} }{ t } } \] | (QGra.LK.2) |
Die beiden unterschiedlichen Halbachsen führen möglicherweise zu zwei Spin-Halbachs-Frequenzen r,pfspin,H; eine je Richtung p.
Für die Frequenz f gilt in Bezug auf die Zeit t erst einmal ganz allgemein:
Für diese Frequenzen ergibt sich dann, wenn rS zur Substitution genutzt wird:
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { _{r}S\;\;\;=\;\;\;\left( 1 - 2 \cdot \frac{G \cdot M}{{_{\raise -.3ex 0}c}^{2} \cdot r} \right) } \] | (QGra.LK.5) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Rightarrow\hspace{10mm}_{r,p}f_{spin,H}\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}c} \cdot {_{r}S^{p}} }{ w_{\raise -.3ex 0} \cdot {_{r}S^{p - \frac{1}{2}}} } } \] | (QGra.LK.6) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}_{r,p}f_{spin,H}\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}c} }{ w_{\raise -.3ex 0} } \cdot {_{r}S^{p - \left( p - \frac{1}{2} \right) }} } \] | (QGra.LK.7) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}_{r,p}f_{spin,H}\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}c} }{ w_{\raise -.3ex 0} } \cdot {_{r}S^{\frac{1}{2}}} } \] | (QGra.LK.8) | ||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}_{r,p}f_{spin,H}\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}c} }{ w_{\raise -.3ex 0} } \cdot \left( 1 - 2 \cdot \frac{G \cdot M}{{_{\raise -.3ex 0}c}^{2} \cdot r} \right)^{\frac{1}{2}} } \] | (QGra.LK.9) | ||
| |||
| \[ \definecolor{formcolor}{RGB}{0,0,0} \color{formcolor} { \Leftrightarrow\hspace{10mm}_{r,p}f_{spin,H}\;\;\;=\;\;\;\frac{ {_{\raise -.3ex 0}c} }{ w_{\raise -.3ex 0} } \cdot \sqrt{ 1 - 2 \cdot \frac{G \cdot M}{{_{\raise -.3ex 0}c}^{2} \cdot r} } } \] | (QGra.LK.10) | ||
Wie wir sehen, fällt die Richtung p weg. Die beiden Effekte, die richtungsabhängige variable Lichtgeschwindigkeit und die richtungsabhängige Veränderung der Geometrie, heben sich auf, wie oben schon vermutet.
So können wir die Formel nun auf einen Umfang u0 beziehen, also für die Spin-Frequenz übernehmen und entsprechend abwandeln:
Die vorstehende Rechnung führe ich im Abschnitt Elementarteilchen im Gravitationsfeld auch für die etwas abweichenden Formeln des Basisteilchenmodells durch. Da das Basisteilchenmodell, anders als die Quanten-Fluss-Theorie und die akademische Physik, nicht zwischen der Elementarteilchen-Spin-Frequenz und der De-Broglie-Frequenz der Elementarteilchen unterscheidet, sondern sogar behauptet, beide wären das Gleiche, wird dort sichtbar, dass das Basisteilchenmodell die De-Broglie-Frequenz im Widerspruch zu den Beobachtungen beschreibt.
XXX XXX XXX XXX XXX XXX XXX XXX
Dieses Ergebnis können wir nutzen, um im Folgenden die Lichtgeschwindigkeitsänderung isotrop, also Richtungsunabhängig, zu beschreiben.
Im Basisteilchenmodell Gieses beschreibt eine Formel dieser Art die De-Broglie-Frequenz der Elementarteilchen, was den experimentellen Beobachtungen widerspricht. In der Quanten-Fluss-Theorie wird die De-Broglie-Frequenz der Elementarteilchen hingegen beobachtungskonform beschrieben.(Link)
Gieses Längenkontraktion im Gravitationsfeld ist korrekt
Die von Giese über den Heaviside-Ellipsoiden hergeleitete Längenkontraktion im Gravitationsfeld der Quantengravitation entspricht der inneren Logik des Elementarteilchen-Modells der Quanten-Fluss-Theorie.
XXX
XXX XXX XXX XXX XXX XXX XXX
XXX
XXX XXX XXX XXX XXX XXX XXX
| → |
|
| |
Lichtbeugung |
|
Eine lokal unterschiedliche Verlangsamung des Lichts erzeugt seine Beugung
| ← |
|
| ▾ | Notizen |
• Eine Herleitung der Lichtbeugung findet sich auch in Variable Lichtgeschwindigkeit in der Allgemeinen Relativitätstheorie, siehe auch Datei "Variable Lichtgeschwindigkeit in der Allgemeinen Relativitätstheorie.pdf".
|
Die Beugung des Lichts oder der Bahn der Lichtteilchen, also der Photonen, kommt auf eine recht einfache Weise zustande:
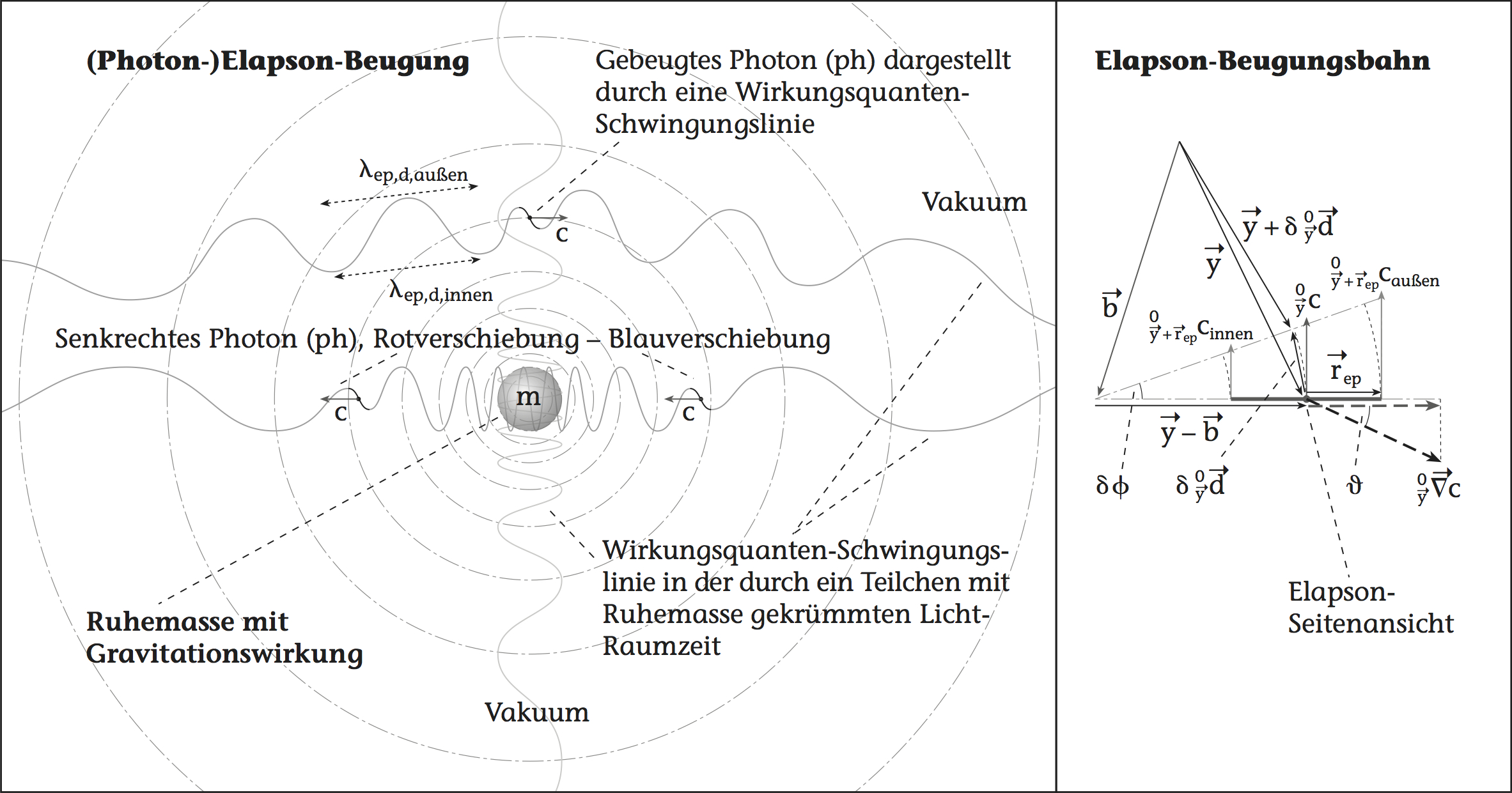
In der Quanten-Fluss-Theorie haben Photonen eine Ausdehnung quer zu ihrer Bewegungsrichtung, eine innere Struktur (siehe und Seite Neue Physik, Abschnitt Elektromagnetische Polarisation, Abbildung 15). Fliegt ein Photon an einer Masse vorbei, dann führt seine Ausdehnung radial zur Masse dazu, dass seine eine Seite der Masse näher ist als seine andere Seite (siehe ).
Durch diesen Effekt ist die der Masse zugewandte Seite einer größeren ausgesetzt, wie im vorhergehenden Abschnitt beschrieben, als seine abgewandte Seite. So wird ein Photon, und jede andere dem Photon ähnliche Struktur – jede lichtähnliche Struktur –, auf eine gebeugte Bahn gezwungen.
Leptonen und alle anderen Elementarteilchen, die nicht Photonen sind, enthalten lichtähnliche Strukturen. Dies führt, wie im beschrieben, zu dem Effekt, den wir Gravitation nennen.
Berechnung der Lichtbeugung
Die sich dadurch ergebende Ablenkung des Lichts durch einen massiven Himmelskörper, wie unsere Sonne, entspricht den Beobachtungen, wie Giese in seiner Arbeit zeigt.
| → |
|
| |
Mechanismus der Gravitation |
|
Gravitation resultiert aus der Beugung lichtähnlicher Strukturen in Elementarteilchen
| ← |
|
|
Die uns im Alltag begegnende Gravitation, also der Grund, warum der Apfel von Baum fällt oder die Planeten um die Sonne kreisen, beruht in der Quanten-Fluss-Theorie, sehr ähnlich wie in Gieses Basisteilchenmodell, auf der dynamischen Struktur der Materie-Elementarteilchen-Strings (Teilchen mit Ruhemasse beziehungsweise Materieinhalt).
Berechnung der Gravitation
Die im Leptonen-Modell (siehe ), als Beispiel, kreisenden lichtähnlichen Strukturen werden bei jeder Rotation in Richtung der anziehenden Masse (siehe ). In der Summe ergibt sich auf diese Weise die gravitative Beschleunigung.
Giese ist es gelungen, die in Experimenten beobachtete und aus der Schule bekannte, klassische gravitative Beschleunigung aus dieser beständigen (Licht-)Beugung in Elementarteilchen zu berechnen.
Im Falle, dass sich das Elementarteilchenmodell der Quanten-Fluss-Theorie insgesamt als mit dem Standardmodell der Teilchenphysik equivalent herausstellt, ergibt sich hierdurch die Vereinheitlichung der Quantenphysik mit der Allgemeinen Relativitätstheorie.
| → |
|
| |
Keine problematische Singularität |
|
Nichts ist wirklich punktförmig, linienförmig oder flächig – alle Strukturen haben eine Ausdehnung
| ← |
|
Eine bemerkenswerte Besonderheit des fraktalen Teilchenmodells der Quanten-Fluss-Theorie besteht darin, dass sowohl die Wirkungsquanten-Strings am Ende nicht wirklich linienförmig als auch die Wirkungsquanten nicht punktförmig sind, sondern sie besitzen prinzipiell eine Ausdehnung.
Aus diesem Grund hat die Quanten-Fluss-Theorie im Prinzip kein Problem mit unphysikalischen Singularitäten; sprich, mit unendlich großer Gravitation zum Beispiel. In der , oberer Teil, erkennt man dies daran, dass die Spitzen des Gravitationsfeldes nach oben hin abgeschnitten sind.
Dies bedeutet nicht, dass die in Näherung hergeleiteten Formeln kein Problem mit Singularitäten haben. Denn es sind ja offensichtlich die Formeln der Allgemeinen Relativitätstheorie, die bekannte Probleme mit Singularitäten beinhalten.
In der Quanten-Fluss-Theorie lassen sich Probleme mit Singularitäten durch genauere Näherungen reduzieren, was in der Allgemeinen Relativitätstheorie zum Beispiel nicht möglich ist.
Die besseren Näherungen werden durch die fraktale Struktur der Quanten-Fluss-Theorie ermöglicht. Diese führen selbstverständlich nur dann zu einer besseren Annäherung an die Realität, wenn die genutzte fraktale Struktur einen nachhaltigen Realitätsbezug besitzt.
Die fraktale Struktur der Wirkungsquanten führt dazu, dass man sich einem Wirkungsquant nicht beliebig annähern kann, ohne das sich sein Erscheinungsbild verändert. Bei Annäherung löst es sich in seine Mikrowirkungsquanten auf, aus denen es besteht. Und dies geht fraktal so zu den immer kleineren Strukturen hin weiter.
| → |
|
| |
Phänomen der Dunklen Materie |
|
Eine erhöhte Vakuum-Energiedichte entfaltet in weiträumig verteilten großen Massen eine zusätzliche Gravitation
| ← |
|
|
|
Bei den oben beschriebenen Berechnungen zur , und zum wurden Vereinfachungen vorgenommen. Diese betreffen nicht nur die , sondern auch die Rolle des Vakuums und seiner Energiedichte in Bezug auf die Gravitation.
Rolle der Vakuum-Energiedichte in der Gravitation
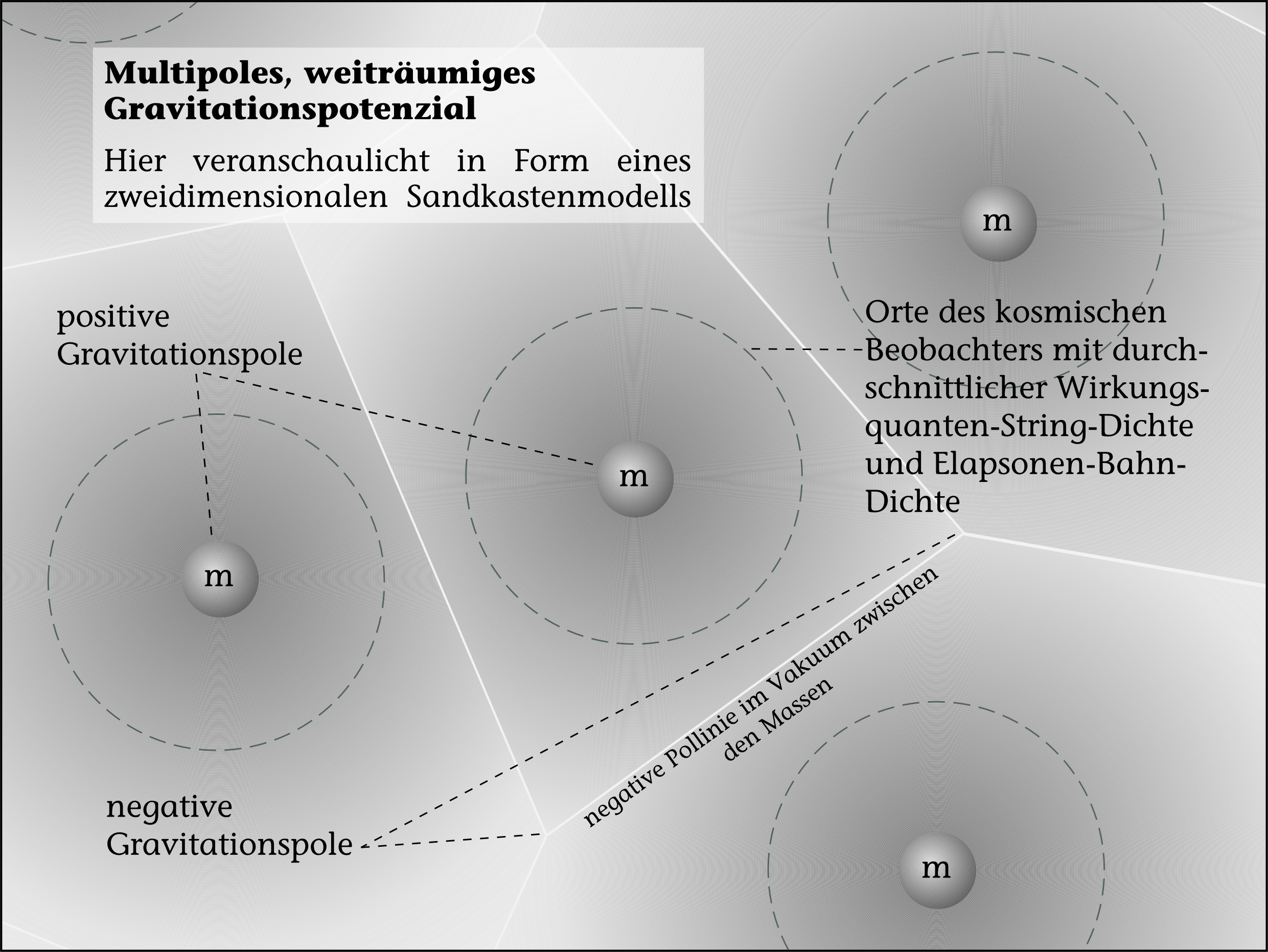
Die mit radialem Abstand veränderliche Vakuum-Energiedichte um eine zentrale Masse bildet das Gravitationspotenzial ab. Um eine Masse herum ist die Vakuum-Energiedichte dabei erhöht und verringert sich nach außen hin.
Weil insgesamt für das Gravitationspotenzial in der Quanten-Fluss-Theorie Energieerhaltung gilt, ist der Energiegehalt des Vakuums um große Massen herum zum Durchschnitt erhöht. Irgendwo zwischen den großen Massen muss er demnach unter dem Durchschnitt liegen.
Durch die unterschiedliche Verteilung der Energiedichte im Vakuum kommt ein zusätzliches Gravitationsphänomen zustande, das der Dunklen Materie.
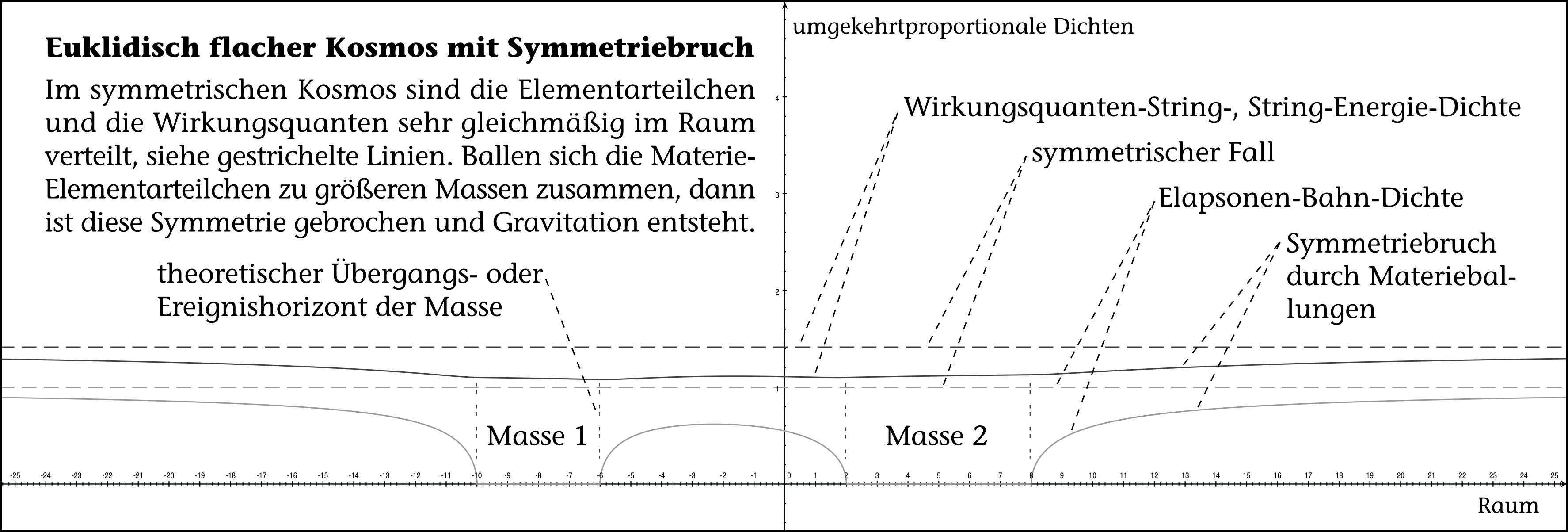
Ohne Symmetriebruch keine Gravitation, aber Graviradiation
Graviradiation hat ihre eigene Existenzberechtigung
Nach der Quanten-Fluss-Theorie gibt es in einem Vakuum, in dem die Energiedichte sehr gleichmäßig verteilt ist, keine Gravitation (siehe ):
Gravitation würde nach der obigen Herleitung bedeuten, es gäbe in Elementarteilchen eine Lichtablenkung, die zu deren Beschleunigung führt. Dies ist bei gleichmäßiger Verteilung der Vakuum-Energiedichte nicht der Fall.
Jedoch wirken die Wirkungsquanten des Vakuums durch die Graviradiation ihrer Impulskegel so aufeinander, dass sich ihre Geschwindigkeit auf die Lichtgeschwindigkeit reduziert. Auf diese Weise entsteht eine innere Bindung des Vakuums.
Dieser symmetrische Fall bedeutet also Graviradiation ohne Gravitation.
Hieran erkennen wir sehr gut, dass die Graviradiation ihre ganz eigene Existenzberechtigung besitzt, weil sie nicht immer gleichbedeutend mit Gravitation ist.
Gravitation entsteht durch einen Symmetriebruch
Bilden sich Massenansammlungen im Vakuum, so ist die Symmetrie der Energiedichteverteilung gebrochen und es entsteht zwischen diesen Gravitation.
Weniger Vereinfachung führt zum Phänomen der Dunklen Materie
Im Fall von Massenansammlungen verschiebt sich aber auch die Verteilung der Vakuum-Energiedichte derart, dass um große Massen herum und im weiträumigen Vakuum innerhalb großer Massenansammlungen die Energiedichte im Verhältnis zum Vakuum zwischen diesen Ansammlungen erhöht ist.
Diese erhöhte Energiedichte führt zu zusätzlicher Gravitation, die wir als Phänomen der Dunklen Materie beobachten, wie das Sandkastenmodell der verdeutlicht.
In ihm werden sogar die negativen Pole der Gravitation sichtbar, die sich im Vakuum zwischen den großen Massen befinden.
Das emergente Verständnis der Quantengravitation in der Quanten-Fluss-Theorie ermöglich das Verständnis der Vakuum-Struktur des Gravitationspotenzials, mit deren Hilfe wir dann besondere Phänomene der Gravitation erkennen können. Das Phänomen der Dunklen Materie ergibt sich auf diese Weise als natürliche Folge der Gravitation, wenn wir genauer hinschauen, indem wir Vereinfachungen auflösen.
| → |
| |
Fußnoten |
|
| 1. |
Vgl. Giulini, Gravitation, Equivalence Principle, and Quantum Mechanics, Kap. 5 Ausblick, S. 14-15. Vgl. Smolin, Die Zukunft der Physik, Kap. 6 Quantengravitation: Am Scheideweg, S. 126-149. Sekundärliteratur: Vgl. Giulini, »Einstein im Quantentest«, S. 62-64. Vgl. Kiefer, »Auf dem Weg zur Quantengravitation«. Vgl. Nicolai, »Auf dem Weg zur Physik des 21. Jahrhunderts«. Internet: Vgl. Wikipedia, Quantengravitation. Vgl. Max Planck Institute for Gravitational Physics, »Relativität und Quanten«. Vgl. Smolin, »Schauspiel auf veränderlicher Bühne«. | |
| 2. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Quantenphysik. | |
| 3. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Quantenfeldtheorie. | |
| 4. |
Vgl. Fließbach, Allgemeine Relativitätstheorie. Vgl. Harrison, Kosmologie, Kap. 8 Allgemeine Relativitätstheorie, S. 253-290. Vgl. Born, Die Relativitätstheorie Einsteins, Kap. VII. Die allgemeine Relativitätstheorie Einsteins, S. 266-324. Vgl. Einstein, »Die Grundlagen der allgemeinen Relativitätstheorie«. Internet: Vgl. Wikipedia, Allgemeine Relativitätstheorie. | |
| 5. |
(Weitere Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Materiewelle. | |
| 6. |
(Primärliteratur einfügen!) Vgl. Harrison, Kosmologie, Kap. 8 Allgemeine Relativitätstheorie, S. 253-290, hier S. 275-278, besonders S. 278. Internet: Vgl. Wikipedia, Zeitdilatation, 2 Zeitdilatation durch Gravitation. Vgl. Wikipedia, Allgemeine Relativitätstheorie, Gravitative Zeitdilatation und Rotverschiebung. | |
| 7. |
Vgl. Schwarzschild, Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Internet: Vgl. Wikipedia, Schwarzschild-Metrik. | |
| 8. | Vgl. Giese, The Origin of Gravity. | |
| 9. | Vgl. Giese, Relativistic Contraction without Einstein!. | |
| 10. |
Im Besonderen erarbeitete, vermutlich als erster, Oliver Heaviside die Kontraktion der Form von in einem Medium oder Äther bewegten, elektromagnetischen Feldern. Die Kontraktion einer bewegten Kugel oder Sphere wurde nach ihm als „Heaviside-Ellipsoid“ benannt: Vgl. Giese, Relativistic Contraction without Einstein!. Vgl. Sexl, Relativität Gruppen Teilchen, S. 96. Vgl. Heaviside, Motion of Electrification through a Dielectric. Vgl. Heaviside, »On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric«. Internet: Vgl. Wikipedia, Lorentzkontraktion. Vgl. Wikipedia, Geschichte der Lorentz-Transformation, Heaviside, Thomson, Searle (1888, 1889, 1896). Vgl. Wikipedia, Michelson-Morley-Experiment, Erklärung, Spezielle Relativitätstheorie. | |
| 11. | Dies muss an anderer Stelle noch explizit aus Gieses Überlegungen hergeleitet werden. Auch Oliver Heaviside soll dazu gearbeitet haben (siehe Motion of Electrification through a Dielectric). | |
| 12. |
Vgl. Fließbach, Allgemeine Relativitätstheorie, Teil III Physikalische Grundlagen der ART, Kap. 12 Gravitationsrotverschiebung, S. 58-64, hier S. 61. Internet: Vgl. Wikipedia, Gravitational redshift, Definition. Vgl. Wikipedia, Ereignishorizont, Bedeutung und Eigenschaften des Ereignishorizonts eines Schwarzen Lochs, Gravitative Rotverschiebung. | |
| 13. | Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier Abbildungen C1, C2, C3, S. 20-21. | |
| 14. |
Internet: Vgl. Wikipedia, Longitudinalwelle. | |
| 15. | Wäre also interessant, ob es in der Akustik einen ähnlichen Effekt gibt. Ich habe etwas in dieser Richtung mal im Spektrum der Wissenschaft gelesen. (Artikel heraussuchen.) | |
| 16. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier Abbildungen C2, C3, S. 21. | |
| 17. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier Abbildungen C1, S. 20. | |
| 18. |
(Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Allgemeine Relativitätstheorie, Grundlegende Konzepte, Raumzeitkrümmung. | |
| 19. |
Internationaler Standard: Vgl. NIST, CODATA Value: speed of light in vacuum. Internet: Wiki einpflegen. | |
| 20. | Hier wird in Polarkoordinaten gedacht: Die tangentiale Koordinate entspricht der Komponente der Lichtbewegung, welche sich nur im Kreis um die Quelle bewegt, die dann nur transversal beeinflusst wird. | |
| 21. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier Formel C.2, S. 21. | |
| 22. | Hier wird in Polarkoordinaten gedacht: Die radiale Koordinate entspricht der Komponente der Lichtbewegung, welche sich nur in Richtung Quelle oder von ihr weg bewegt, welche dann nur longitudinal beeinflusst wird. | |
| 23. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier S. 21. | |
| 24. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier Formel C.3, S. 21. | |
| 25. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier Formel C.4, S. 21. | |
| 26. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier Formel C.4, S. 21. | |
| 27. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier S. 22. | |
| 28. | Vgl. Wikipedia, Plancksches Wirkungsquantum, Definition. | |
| 29. | Vgl. Wikipedia, Plancksches Wirkungsquantum, Definition. | |
| 30. |
Vgl. Einstein, »Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?«. Internet: Vgl. Wikipedia, Äquivalenz von Masse und Energie. | |
| 31. | Vgl. Wikipedia, Standardabweichung. | |
| 32. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier S. 22. | |
| 33. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, S. 19-22, hier Formel C.5, S. 22. | |
| 34. |
Vgl. Schwarzschild, Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie. Internet: Vgl. Wikipedia, Schwarzschild-Metrik. | |
| 35. |
Vgl. Giese, The Origin of Gravity, Kap. 2 Bending of a Beam of Light Passing a Massive Object, S. 1-4, hier Formel 2.1, S. 1. Diese Formel kann man aus der Veränderung der Detektorwellenlänge der Schwarzschild-Lösung herleiten: Vgl. Harrison, Kosmologie, Kap. 9 Schwarze Löcher, S. 291-323, hier S. 295, ergänzendes S. 297, 320. Internet: Vgl. Wikipedia, Gravitational redshift, Definition. | |
| 36. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 13.1 Ansatz zur quantitativen Formulierung der Lichtgeschwindigkeit im Gravitationspotenzial, S. 141-149, hier Formel 13.17, S. 145. Dort hat die Formel noch eine leicht andere Form. | |
| 37. |
Vgl. Shapiro, »Fourth Test of General Relativity«. Internet: Vgl. Wikipedia, Shapiro-Verzögerung. | |
| 38. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, Speed Reduction in Detail, S. 20-22, hier Formel C.7, S. 22. N steht darin nicht für die Masse einer kugelförmigen Ansammlung von Elementarteilchen, sondern N steht für die Anzahl der Basisteichen, also für die doppelte Anzahl der Elementarteilchen. | |
| 39. | Eine genaue Herleitung der unbekannten Konstanten wird gesucht. Hinweise darauf sind erbeten. | |
| 40. |
Im Besonderen erarbeitete, vermutlich als erster, Oliver Heaviside die Kontraktion der Form von in einem Medium oder Äther bewegten, elektromagnetischen Feldern. Die Kontraktion einer bewegten Kugel oder Sphere wurde nach ihm als „Heaviside-Ellipsoid“ benannt: Vgl. Giese, Relativistic Contraction without Einstein!. Vgl. Sexl, Relativität Gruppen Teilchen, S. 96. Vgl. Heaviside, Motion of Electrification through a Dielectric. Vgl. Heaviside, »On the Electromagnetic Effects due to the Motion of Electrification through a Dielectric«. Internet: Vgl. Wikipedia, Lorentzkontraktion. Vgl. Wikipedia, Geschichte der Lorentz-Transformation, Heaviside, Thomson, Searle (1888, 1889, 1896). Vgl. Wikipedia, Michelson-Morley-Experiment, Erklärung, Spezielle Relativitätstheorie. | |
| 41. | Vgl. Giese, Relativistic Contraction without Einstein!. | |
| 42. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, Speed Reduction in Detail, S. 20-22, hier in der Entwicklung der Formel C.8, S. 22. | |
| 43. | Vgl. Giese, The Origin of Gravity, Appendix C Variation in the Speed of Light, Speed Reduction in Detail, S. 20-22, hier Formel C.8, S. 22. Die erste Variable rechts neben dem Gleichheitszeichen $ w_{0} $ ist dort mit $ r $ benannt. Diese Benennung ist fehlerhaft, weil es eine weitere Variable $ r $ unter dem Bruch gibt, die von der ersten unabhängig ist. Beide müssen also unterschieden werden, weil die erste neben dem Gleichheitszeichen eine generelle geometrische Ausdehnung von Strukturen meint, während die zweite den Abstand vom Zentrum einer Zentralmasse bedeutet. Folgerichtig habe ich dann die Variable $ r_{red} $ bei Giese in $ d_{red} $ umbenannt, weil diese die Reduktion der Ausdehnung einer generellen Struktur meint. Die Konstante $ c $ habe ich wegen der Eindeutigkeit in $ c_{0} $ umbenannt. | |
| 44. |
(Weitere Primärliteratur einfügen!) Internet: Vgl. Wikipedia, Materiewelle. | |
| 45. |
Vgl. Shapiro, »Fourth Test of General Relativity«. Internet: Vgl. Wikipedia, Shapiro-Verzögerung. | |
| 46. | Vgl. Giese, The Origin of Gravity, 2 Bending of a Beam of Light Passing a Massive Object, S. 1-3, hier S. 3. Und: Appendix A, Mathematical Deduction of the Refraction Process, S. 14-17. | |
| 47. | Vgl. Huß, Die Gravitonen-Fluss-Theorie, v7.381, Kap. 5.3.2 Wechselwirkung von potenzialen Photonen-Beugungssystemen, S. 103-109, hier S. 104. | |
| 48. | Vgl. Giese, The Origin of Gravity, 3 Relationship between Gravity and the Basic Particle Model, S. 4-6, hier S. 5-6. |
| |
Stand 13. Februar 2025, 18:00 CET.
-
Permanente Links:
(Klicke auf die Archivlogos
zum Abruf und Ansehen
der Archive dieser Seite.) -

-
archive.todaywebpage capture